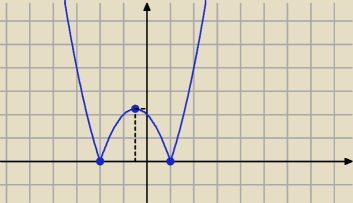
PW: min|u| = 0 i minimum to jest osiągane, gdy u = 0.
Znaleźć miejsca zerowe wyrażenia u(x) = x
2 + x − 2. W tych punktach funkcja osiąga minimum
równe 0, i jest to minimum zarówno lokalne jak i globalne.
| | 1 | |
Funkcja u(x) osiąga minimum lokalne m dla x0 = − |
| i jest ono ujemne (trzeba je |
| | 2 | |
policzyć), stąd wynika w sposób oczywisty, że funkcja |u(x)| ma w tym punkcie maksimum lokalne
równe −m (jest to liczba dodatnia).