:) Ona : Hejka. Musze wyznaczyć przedziały monotoniczności funkcji

	x2+1
y=
	x+1

1.D;x∊R/{−1}

	x2+2x−1
2.y`=		D=D`
	(x+1)2

	x2+2x−1
3.		=0 i tu moje pytanie, czy mogę pomnożyć obustronnie przez (x+1)2 i wtedy
	(x+1)2

mam równanie kwadratowe do obliczenia ?

J: masz zbadać znak pochodnej , ... zauważ,że mianownik jest zawsze dodatni ...

rafal:

	a
Ułamek		=0 ⇔ a=0. (b≠0)
	b

Możesz przyrównać licznik do 0, znalezione x to będą ekstrema

J: tu nie szukamy ekstremów, tylko monotoniczność...

rafal: co nie znaczy, że wskazówka się nie przydała. Mając ekstrema już 1 krok od wyznaczenia monotoniczności

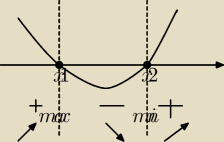
Ona : Reasumując: x²+2x−1=0 (x+1)²≠0 Δ=8 √Δ=2√2

	−2−2√2
x1=		≈−2,4
	2

	−2+2√2
x2=		≈−0,4
	2

Ona : Trochę niewyraźny obrazek, ale wydaje mi się, że to dobrze zrobiłam

Ona : Potem jeszcze mogę obliczyć minimum w pkt i maksimum w pkt podstawiając x1 i x2 pod funkcję

rafal: pamiętaj, że to nie jest wykres funkcji y ale przedziały monotoniczności wyznaczone. Na kolokwium albo zostawisz tabelkę jako odpowiedź, albo zapiszesz, że y maleje dla x∊... itd

rafal: Niekoniecznie będą to wartości minimalne i maksymalne. Można je też otrzymać zmierzając iksem do minus i plus nieskończoności. W poleceniu tym bardziej nie było wymagane, żeby je wyznaczyć, ale tak, lokalnie tak własnie je otrzymasz

Ona : f(x)↗dla x∊(−∞,−2,4)u(−0,4,∞) f(x)↘dla x∊(−2,4 ; −0,4)

Ona : Czyli rachunkowo wszystko dobrze zrobilam ?

rafal: Jeśli naprawdę mogę się jeszcze czegoś uczepić, to tego, ze w matematyce nie przybliżamy.

	−2−2√2		2(−1−√2)
x1=		=		=−1−√2 a nie −2,4. x2 analogicznie. Także odpowiedź
	2		2

f(x)↗ dla x∊(−∞,−1−√2)∪(−1+√2,∞)

Ona: Dziekuje