Funkcja Ksaweryx: Wyznacz największą oraz najmniejszą wartość funkcji f(x)= −3x²−8x+4 w przedziale <−2;1>

Janek191: f(x) = − 3 x² − 8 x + 4 < − 2; 1 >

	8		4
p =		= −		∊ < − 2; 1 >
	− 6		3

i a = − 3 < 0 ( ramiona paraboli skierowane są ku dołowi ) więc

	4		16		−4		16		32		12
ymax = f(p) = f( −		) =− 3*		− 8*		+ 4 =−		+		+		=
	3		9		3		3		3		3

	28		1
=		= 9
	3		3

y_min = f(1) = − 3*1 − 8*1 + 4 = − 7

Ksaweryx: ale to w przedziale<−2;1> czyli bedzie wynik −2 i 1 tak ?

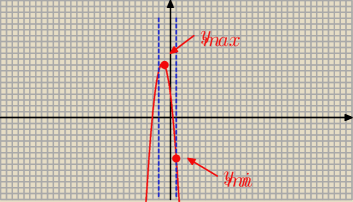
Janek191: Nie :

	1
największa wartość , to 9
	3

najmniejsza wartość, to − 7 Patrz na wykres