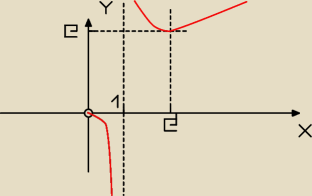
Na rysunku poniżej masz narysowaną pewną funkcję.
Kiryoku:
Krótko opisz:
a) dziedzinę funkcji
b) przedziały monotoniczności funkcji
c) ekstrema funkcji
d) znajdź dla funkcji najmniejszą wartość w przedziale (0,e>
3 gru 22:51
Kiryoku: wiem, że rysunek jest kiepskiej jakości, jeżeli ktoś chce zobaczyć oryginał wyślę mailowo.
Proszę o pomoc.
3 gru 22:56
Kiryoku: z tym, że (0,0) nie należy do wykresu, powinno byc zaznaczone kółko otwarte
3 gru 23:03
3 gru 23:05
Kiryoku: D= (0,1) i (1,∞)?
funkcja jest przedziałami monotoniczna
malejąca w przedziale od (0.1) i (1,e>
rosnąca w przedziale od <e, ∞)
3 gru 23:13
Kiryoku:
3 gru 23:14
Kiryoku: nie umiem rysować
Nie bardzo wiem jak miałbym okreslić ekstreme i okreslić najmniejszą wartość w przedziale od
(o,e>
3 gru 23:15
Kiryoku: Krystek, jesteś jeszcze?
3 gru 23:24
Kiryoku: Proszę o pomoc
3 gru 23:43
Kiryoku: Na przesłanie pracy mam jeszcze dziesięć minut
3 gru 23:47
stróż:
ale to nie będzie Twoja praca
3 gru 23:48
Eta:
To już zaczynaj wylewać "krokodyle łzy"
3 gru 23:48
Kiryoku: Tak też myślałem... Ech. trudno. a możesz mi powiedzieć czy to jest poprawnie?
D= (0,1) i (1,∞)
funkcja jest przedziałami monotoniczna malejąca w przedziale od (0.1) i (1,e>
rosnąca w przedziale od <e, ∞)
3 gru 23:49
Eta: ok
3 gru 23:50
Kiryoku: a tak na szybciutko może chociaż ekstreme pomożesz mi policzyć?
3 gru 23:51
Lukas:
Poczekam jeszcze 5 minut
3 gru 23:56
Mila:
1) D=(0,1)∪(1,∞)
2) f(x) jest malejąca w przedziałach: (0,1), (1,e)
f(x) rosnąca dla x∊(e,∞)
3) W punkcie (e,e) funkcja ma minimum : f(e)=e
4) f(x) ma w przedziale (1,e> ma wartość namniejszą równą e.
3 gru 23:56
Eta:
Mila idź już spać
3 gru 23:58
Kiryoku: ... W ostatnich sekundach dałem radę wysłać...
Mila, jak odpowiedziałaś na 3 i 4?
3 gru 23:59
Kiryoku: w sensie, jak można było stwierdzić taką odpowiedź? np w 3?
Dlatego że wynika to z twierdzenia ekstremu>
A w 4?
4 gru 00:02
Kiryoku: w każdym bądź razie bardzie dziękuje za pomoc Dorbanoc
4 gru 00:09