Trygonometria: Równanie Jacek: cos(pi/4 − x) = (sqrt 2)/3

Mila: Może tak:

	π		√3
cos(		−x)=		?
	4		2

Jacek: Niestety, ale 2 jest pod pierwiastkiem

Mila: ⇔

	π		√2
cos(x−		)=
	4		3

Albo odczytujesz przybliżenie dla jakiego α cosinus jest równy U{√2{3} albo korzystasz z arccos x. To zależy do czego potrzebne rozwiązanie.

Jacek: Okay, postaram się tak rozwiązać. Mam też jeden problem z takim przykładem. sin(x−pi/3)=−1/2 t=x−(pi/3) sint=−1/2 t=−pi/6 Następnie chce obliczyć tą niewiadomą i wychodzi mi taka (chyba) głupota. x−(pi/3)=−pi/6 + 2kpi x=−pi/6+(2pi/6) + 2kpi i x=pi/6, a według autora poprawną odpowiedzią jest: x=−pi/2 + 2kpi, x=pi/6 +2kpi, k E C

Mila:

	π		1
sin(x−		)=−		⇔
	3		2

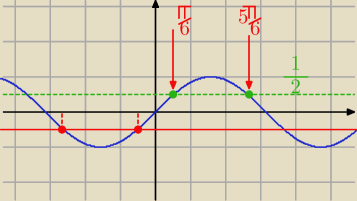
Masz serię rozwiązań:

	π		π		π		−5π
x−		=−		+2kπ lub x−		=		+2kπ⇔
	3		6		3		6

	π		π		π		5π
x=		−		+2kπ lub x=		−		+2kπ⇔
	3		6		3		6

	π		π
x=		+2kπ lub x=−		+2kπ
	6		2

Jacek: Dziękuje

Mila:

Jacek: Chciałbym powrócić jednak do tego przykładu: cos(pi/4 − x) = (sqrt 2)/3 //sposób z przybliżeniem w odpowiedzi od autora jest takie cudo: x=2kpi, x=pi/2 +2kpi mi natomiast wychodzi x= −pi/12 x=−1*5/12

Mila: wg odpowiedzi powinno być takie równanie:

	π		√2
cos(		−x)=
	4		2

Jacek: Zgadza się, moja pomyłka, spojrzałem na przykład obok.

Jacek: Mimo wszystko otrzymałem identyczne odpowiedzi