pomocy zadanie z geometrii o czworokącie
majza: W czworokącie wypukłym suma długości przekątnych jest równa 20cm, a kąt ostry pomiędzy
przekątnymi ma miarę 45 stopni. Wyznacz długość przekątnych, dla których pole tego czworokąta
jest największe z możliwych. Proszę, aby w miare jasno opisać, bo chciałabym wszystko
dokładnie zrozumieć
3 gru 17:35
majza: proszę bardzo mi zależy pls pls
3 gru 17:41
majza: up
3 gru 17:44
===:
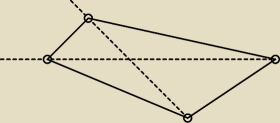
znasz wzór na pole trójkąta z sinusem kąta między bokami ? −
3 gru 17:49
===:
... no tak ... czekasz na gotowca −
3 gru 18:04
majza: no prosiłabym, nie jestem dobra z matmy
3 gru 18:24
===:
zadałem Ci pytanie ... poszukaj tego wzoru
3 gru 18:28
3 gru 18:29
majza: bok razy bok razy sinus kąta, tak ?
3 gru 18:33
===: tak
3 gru 18:34
majza: no i co mam z ta informacja zrobic ? jak zaczac ?
3 gru 18:42
===:
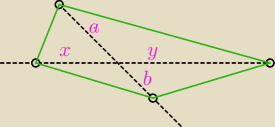
P=0,5sin45
o*ax+0,5sin135
o*ay+0,5sin45
o*by+0,5sin135
o*bx
| | √2 | | √2 | | √2 | |
P= |
| (ax+bx+ay+by)= |
| {x(a+b)+y(a+b)}= |
| (a+b)(x+y) |
| | 4 | | 4 | | 4 | |
3 gru 18:49
===:
jeśli oznaczysz przekątne jako p i q gdzie p=a+b q=x+y
i wiesz, że p+q=20 ⇒ q=20−p
wtedy:
| | √2 | |
P= |
| p(20−p) .... i szukasz pw ....dla którego Pmax |
| | 4 | |
3 gru 18:58
majza: ok dzięki
3 gru 19:14
===:
... i co wyszło?
3 gru 19:18