Wykaż, że: a). jeśli przekątne prostokąta są dwusiecznymi jego kątów, to prostok KBA: Witam wszystkich forumowiczów. Zadania z wyrazem "wykaż" od samego początku budzę we mnie mieszane uczucia bo nie potrafię sobie z nimi poradzić. Oto moje zadanie: Wykaż, że: a). jeśli przekątne prostokąta są dwusiecznymi jego kątów, to prostokąt jest kwadratem, b). jeśli przekątne rombu są równej długości, to romb jest kwadratem. Do podpunktu "a" zrobiłem rysunek. Widzę, że przekątne przecinają się pod kątem prostym. Powstałe trójkąty mają te same pole.

===: na przeciwko równych kątów... leżą równe boki ... i powalcz −

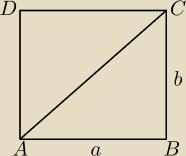
irena_1: a) Jeśli AC jest dwusieczną kąta DAB i kąta BCA, to kąty CAB i CBA mają po 45⁰, czyli trójkąt ABC jest równoramiennym trójkątem prostokątnym, więc a=b. Wniosek− taki prostokąt ma równe boki, czyli jest kwadratem

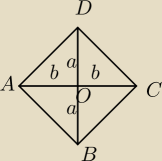
irena_1: b) Jeśli romb ma równej długości przekątne, to a=b, czyli wszystkie trójkąty: AOB, BOC, COD, AOD są równoramiennymi trójkątami prostokątnymi, czyli kąty: OAB, OBA, OBC, OCB, OCD, ODC, OAD, ODA mają po 45⁰, a stąd kąty rombu mają po 90⁰, są kątami prostymi. Stąd− taki romb jest kwadratem