geometria analityczna zadanie z trapezem Karolina: Proszę o pomoc punkty A(0 −5) oraz D(−3 −1) są kolejnymi wierzchołkami trapezu równoramiennego abcd,którego osią symetrii jest prosta o równaniu x+2y=0. Oblicz współrzędne pozostałych wierzchołków oraz długość odcinka łączącego środki ramiontego trapezu.

M:

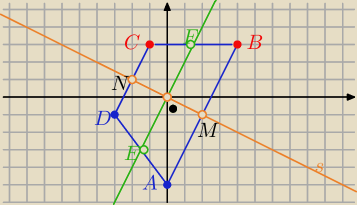
Eta: s : y= −0,5x to prosta AB⊥s : y=2x−5 ⇒ M=(2,−1) to B=(4,3) i |AB|=a=4√5 analogicznie dla podstawy DC: s: y=−0,5x DC:y= 2(x+3)−1 ⇒ DC: y=2x+5 ⇒ N=(−2,1) to C=(−1,3) i |DC|=b=2√5

	a+b
|EF|=		= 3√5
	2

#k: Można prosić o rozwiązanie za pomoca wektorów ? Dziękuje

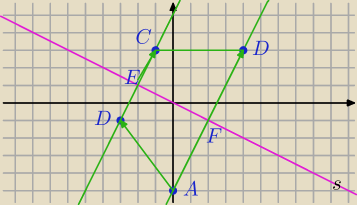
Mila: 1) oś symetrii trapezu:

	1
s: x+2y=0 ( ⇔s : y=−		x )
	2

D=(−3,−1) DC⊥s i D∊prostej DC DC: 2x−y+C=0 i 2*(−3)−(−1)+C=0⇔C=5 DC: 2x−y+5=0 (y=2x+5 ) 2) E− Punkt przecięcia DC i s

	1
−		x=2x+5
	2

E=(−2,1) , DE^→=[1,2] E=(−2,1)→T_[1,2]⇒C=(−2+1,1+2)⇔C=(−1,3) DC^→=[2,4] |DC|=√2²+4²=√20=2√5 3) PUNKT B AB ||DC i A=(0,−5)∊AB 2x−y+C=0 , 2*0−(−5)+C=0, C=−5 AB: 2x−y−5=0 (y=2x−5) F− Punkt przecięcia z prostą s

	1
2x−5=−		x
	2

F=(2,−1), AF^→=[2,4] AB^→[4,8] A=(0,−5)→T_[4,8]⇒B=(4,3) |AB|=√16+64=√80=4√5 4) Dł. odcinka łączącego środki ramion tego trapezu.

	2√5+4√5
d=		=3√5
	2

#k: Dziękuje Milu