Trójkąt równoboczny
dipsi: Dany jest trójkąt równoboczny ABC o boku długości 16. Na boku BC obrano punkt K dzielący ten
bok w stosunku 3:5 licząc od punkty B. wyznacz sinus kąta BAK i pole trójkąta BAK.
AK=y CK=5x KB=3x
5x+3x=16
x=2
z twierdzenia cosinusów moje y=14 i nie wiem jak policzyć sinus kąta BAK.
Próbowałam z twierdzenia cos, cos BAK i wyszło na to że jest równy 1.
proszę o pomoc tylko z tym sinusem
2 gru 21:01
Eta:
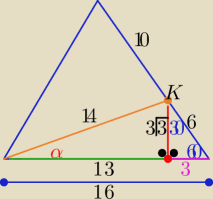
sinα=...........
2 gru 21:15
Bogdan:
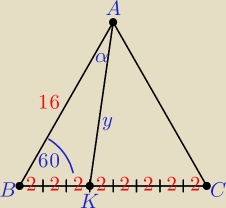
Z twierdzenia cosinusów w trójkącie ABK obliczamy wartość y.
| | 1 | | 1 | |
Pole trójkąta ABK P = |
| *16*6*sin60o i jednocześnie P = |
| *16*y*sinα |
| | 2 | | 2 | |
2 gru 21:16
pigor: ... z porównania wzorów na pole ΔBAK :
h
BC=
12*16
√3= 8
√3 ⇒
12*6*8
√3=
12*14*16sin(BAK) ⇔
⇔ 3
√3= 14sin(BAK) ⇒
sin(BAK)= 314√3 . ..
2 gru 21:16
dipsi: z czego obliczamy 13 i 3√3?
2 gru 21:16
Eta:
2 gru 21:16
===:
z twierdzenia sinusów
2 gru 21:18
Eta:
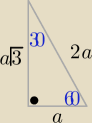
Z trójkąta "ekierki" o kątach 30
o,60
o, 90
o
2 gru 21:18
dipsi: już wszystko wiem, dziękuje
2 gru 21:19
Eta:
−−−−−−=3 to −−−−−−−−−−−−−−−− = 16−3=13
2 gru 21:20