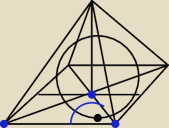
 a=5Δssss
a=5Δssss
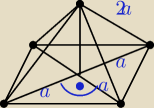 a)przekrój jest trójkątem równobocznym
długość przekątnej podstawy : 2a
długości krawędzi bocznych: 2a
długość krawędzi podstawy: a√2
Pole podstawy: Pp=2a2
wysokość ostrosłupa: H2=(2a)2−a2
H=a√3
objętość ostrosłupa:
a)przekrój jest trójkątem równobocznym
długość przekątnej podstawy : 2a
długości krawędzi bocznych: 2a
długość krawędzi podstawy: a√2
Pole podstawy: Pp=2a2
wysokość ostrosłupa: H2=(2a)2−a2
H=a√3
objętość ostrosłupa:
| 1 | ||
V= | *2a2*a√3 | |
| 3 |
| 2a3 | ||
V= | √3 | |
| 3 |
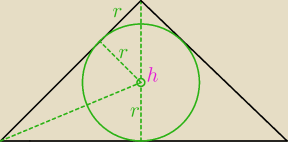 b)
h=r+√2r=r(1+√2)
b)
h=r+√2r=r(1+√2)
| 2h | ||
2h=a√2 ⇒ a= | =h√2=√2r+2r | |
| √2 |
| 1 | 1 | |||
Vo= | (√2r+2r)2(r+√2r)= | (6r2+4√2r2)(r+√2r)= | ||
| 3 | 3 |

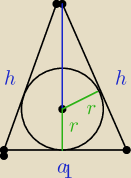
| a2 | 7a2 | 14a2 | √14a | |||||
h2=4a2− | = | = | −−−> h= | |||||
| 2 | 2 | 4 | 2 |
| √14a | ||
a√2*a√3=r* | ||
| 2 |
| 2a√3 | ||
r= | ||
| √7 |
| 4 | 4 | 4 | 24a3√3 | 32a3√3 | ||||||
Vk= | πr3= | π= | * | = | ||||||
| 3 | 3 | 3 | 7√7 | 7√7 |
| Vk | |
=... | |
| Vo |
 "przekrój ostrosłupa zawierający dwie jego krawędzie boczne jest trójkątem:b) prostokątnym
"przekrój ostrosłupa zawierający dwie jego krawędzie boczne jest trójkątem:b) prostokątnym