Planimetria trójkąt kleocat: Dwa boki trojkata maja dlugosc a i b. Znajdz dlugosc trzeciego boku jezeli kat lezacy naprzeciw tego boku jest dwa razy wiekszy od kata lezacego naprzeciw boku a. Z moich wyliczen wyszlo c = 2*a*cosα a = b/cos2α b = a*cos2α

kleocat: nie wiem co dalej potrzebna pomoc

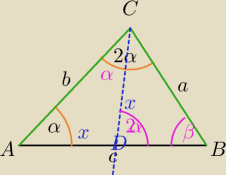
Mila: I sposób Prowadzimy dwusieczną kąta ACB: ΔADC−Δrównoramienny−AD=CD Z tw o dwusiecznej mamy:

	b		a
(1)		=
	x		c−x

ΔCDB∼ΔABC⇔

	a		c
(2)		=		⇔c*(c−x)=ab
	c−x		b

Z obu równań:

b		c
	=
x		b

	b2
x=		podstawiamy do (2)
	c

	b2
c*(c−		)=ab
	c

	c2−b2
c*		=ab⇔
	c

c²−b²=ab c²=b²+ab c=√b*(a+b) ========= II sposób β=180−3α Z tw. sinusów:

a		b		c
	=		=
sinα		sin(3α)		sin(2α)

a		c		a		c
	=		⇔		=		⇔
sinα		sin(2α)		sinα		2sinα*cosα

	c		b
a=		=
	2cosα		sin3α

oblicz cos α