planimetria operon Olgaaa: 1. Dany jest trójkąt ABC. Odcinki DE i FG są równoległe do boku AB trójkąta i G, E ∊ AC. Stosunek pól figur DEC, DEGF i ABGF w podanej kolejności jest równy 7:2:6. Ile równy jest

	|GF|
stosunek		?
	|AB|

2. Dany jest trójkąt równoramienny ABC, w którym kąt między ramionami AC i BC ma miarę 2α. Promień okręgu wpisanego w ten trójkąt ma długość r. Wyznacz obwód i pole tego trójkąta.

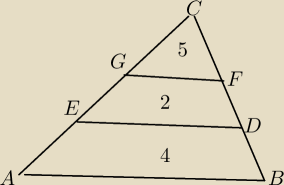Ditka: stosunek pola ΔDEC do pola trapezu DEGF jest 7:2, więc jeśli pole ΔDEC wynosi 7 jednostek a trapezu DEGF 2 jednostki to pole ΔFGC 7−2=5 jednostek. Tak samo wnioskujemy,że pole trapezu ABDE wynosi 6−2=4 jednostki GF− podstawa ΔGFC AB− podstawa ΔABC ΔGFC∼ΔABC pole ΔABC=5+2+4=11 pole ΔGFC do pola ΔABC jest w stosunku 5:11 i to jest kwadrat skali podobieństwa więc

|GF|
	=√511
|AB|

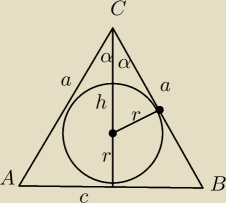Ditka: h− wysokość ΔABC P=¹₂*c*h

	r
sinα=
	h−r

sinα(h−r)=r

	r(1+sinα)
h=
	sinα

	c2
tgα=
	h

	r(1+sinα)
c=2*h*tgα=2*		*sinαcosα
	sinα

	r(1+sinα)
c=2*
	cosα

	r2(1+sinα)2
P=
	sinα*cosα

	c2
sinα=
	a

	c
a=
	2sinα

	r(1+sinα)
a=
	sinα*cosα

obwód:

	r(1+sinα)		r(1+sinα)		2r(1+sinα)+2r(1+sinα)sinα
2a+c=2		+2*		=		=
	sinα*cosα		cosα		sinα*cosα

2r(1+sinα)(1+sinα)		2r(1+sinα)2
	=
sinα*cosα		sinα*cosα

jaga: P=p*r

	2P
Ob= 2p=
	r

Olgaaa: Dziękuję