| 1 | 1 | |||
Obliczmy limx→1− | =limx→1−(− | )= | ||
| 1−x3 | (x−1)(x2+x+1) |
| 1 | ||
=− | =+∞ | |
| 0−*3 |
| 1 | 1 | |||
limx→1+ | =limx→1+(− | )= | ||
| 1−x3 | (x−1)(x2+x+1) |
| 1 | ||
=− | =−∞ | |
| 0+*3 |

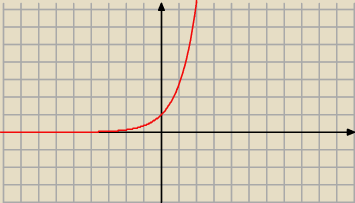 Funkcja y=ex wygląda jak na rysunku, widać, że limx→+∞ex=+∞, a limx→−∞ex=0. Policzyłem
granicę lewostronną i prawostronną wykładnika, a potem skorzystałem z tej własności.
Funkcja y=ex wygląda jak na rysunku, widać, że limx→+∞ex=+∞, a limx→−∞ex=0. Policzyłem
granicę lewostronną i prawostronną wykładnika, a potem skorzystałem z tej własności.
 tylko nie rozumiem jednej rzeczy dlaczego:
tylko nie rozumiem jednej rzeczy dlaczego:
| 1 | ||
− | =+∞ | |
| 0−*3 |
| 1 | 1 | 1 | ||||
Ułamek typu | dąży do −∞, np. | =−1000 itd. Jeżeli masz − | to masz | |||
| 0− | −0,001 | 0−*3 |
| 1 | ||
2 minusy, stąd +∞. Np − | =333,33333333333333333333333333333, bardzo dużo, prawda? | |
| −0,001*3 |
