PARAMETR 155178: f(x)=1+sin(−X)+cos(^π₂+x) DLA JAKIEGO m <<<<<<f(x)=m>>>>>>> równanie podane wyżej ma 2 rozwiązania w przedziale <π;2π> ?

155178: @

155178: #

155178: @

155178: #

155178: #

155178: #

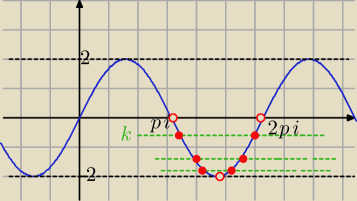
Eta: f(x)= 1−sinx−sinx= 1−2sinx 1−2sinx= m ⇒ 2sinx=1−m f(x)= 2sinx , g(x)= k k= 1−m to k∊(−1,0) ⇒ 1−m> −1 ⋀ 1−m<0 dokończ......

155178: czemu k∊(−1;0) jeśli z rysuneczku wychodzi od (−2;0) ?

Eta: Przez pomyłkę wpisałam ma być k∊(−2,0)

155178: Dzięki A będzie otwarte czy zamknięte ? Bo w dziedzinie jest przedział zamknięty <π;2π>, czyli wydaje mi się , że te dwa zera na π,2π też będą w odpowiedzi ?

155178: Wynik powinien wyjść m<1;3> ?

pigor: ..., a więc f(x)= 1+sin(−x)+cos(^π₂+x) ; dla jakiej wartości parametru m równanie f(x)=m ma 2 rozwiązania w przedziale <π;2π> ? −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− otóż, równanie f(x)= m ⇔ 1−sinx−sinx= m ⇔ 1−m= 2sinx ⇔ ⇔ sinx=¹₂(1−m) ma 2 rozwiązania w <π;2π> ⇔ −1≤ sinx≤ 0 ⇔ ⇔ −1≤ ¹₂(1−m)≤ 0 /*2 ⇔ −2≤ 1−m≤ 0 ⇔ −3≤ −m ≤< −1 ⇔ ⇔ 3 ≥m ≥1 ⇔ 1≤ m≤ 3 ⇔ m∊[1;3] . ..

.....:: Dla m=3 w przedziale <π, 2π> jest tylko jedno rozwiązanie