Pare zadań z rachunku
Sins23: 1Wiadomo że P(AnB')=P(BnA'), P(AUB)=34 P(AnB)=14. Oblicz P(B), P(A\B)
2Grupa składająca się z 6 osób siada w sposób losowy wokół okrągłego stołu. Oblicz
prawdopodobieństwo że dwie z góry ustalone osoby
a) wsiądą obok siebie
b) nie będą sasiadować ze sobą
3 W dzudziestosobowej klasie, w której jest 6 dziewczyn, rozlosowano 5 biletów do teatru. Jakie
jest prawdopodobieństwo, że wśród posiadaczy biletów znajdą się dokładnie dwie dziewczyny
1 gru 18:02
Sins23: Pomoże ktoś

? w 2 a) jest 'usiądą'
2 gru 00:35
Gustlik:
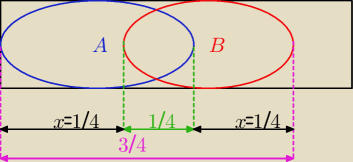
Z rysunku:
Niech P(AnB')=P(BnA')=x,
P(AUB)=34 P(AnB)=14. Oblicz P(B), P(A\B)
8x+1=3
8x=2 /:8
2 gru 00:54
Gustlik:
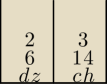
3 W dzudziestosobowej klasie, w której jest 6 dziewczyn, rozlosowano 5 biletów do teatru. Jakie
jest prawdopodobieństwo, że wśród posiadaczy biletów znajdą się dokładnie dwie dziewczyny
Metoda "przegródkowa" − patrz rysunek
2 gru 01:01
Gustlik: 2Grupa składająca się z 6 osób siada w sposób losowy wokół okrągłego stołu. Oblicz
prawdopodobieństwo że dwie z góry ustalone osoby a) wsiądą obok siebie b) nie będą sasiadować
ze sobą
|Ω|=6!
ad a)
Możliwe ustawienia:
ABxxxx
xABxxx
xxABxx
xxxABx
xxxxAB
BxxxxA (bo to okrągły stół i ostatnie miejsce jest obok pierwszego)
Ponieważ osoby A i B mogą usiąść w odwrotnej kolejności (czyli BA) będzie tyle samo ustawień
dla kolejności BA, zatem mamy:
|A| = 6*2*4!=... (4! to ustawienia pozostałych osób oznaczonych jako x)
P(A)=...
ad b) Zdarzenie B=A', zatem |B|=|Ω|−|A|.
2 gru 01:07
kyrtap: P(AnB')=P(BnA') ⇒ P(AnB')=P(BnA') = P(A\B) = P(B\A)
Skorzystam teraz z aksjomatów prawdopodobieństwa :
(A\B) ∪ (B\A) ∪ (A∩B) = A∪B
(A\B),(B\A),(A∩B) − parami rozłączne
P(A\B) + P(B\A)+ P(A∩B) = P(A∪B)
P(B\A) + P(B\A) + P(A∩B) = P(AUB)
2P(B\A) = P(AUB) − P(A∩B)
| | 3 | | 1 | | 1 | |
2P(B\A) = |
| − |
| = |
| |
| | 4 | | 4 | | 2 | |
2 gru 01:11
Gustlik: kyrtap, dobra metoda, ale ta z rysunku jest czytelniejsza, nie trzeba znać wzorów, liczysz
graficznie i widzisz, co robisz. Uczniowie ją lubią, bo jest przejrzysta. Poza tym te
aksjomaty wzięły się właśnie z takich rysunków.
2 gru 01:21
kyrtap: po prostu ja się lubię aksjomatami posługiwać w takich zadankach

2 gru 13:03
Gustlik: kyrtap No i ok, niech uczniowie znają kilka sposobów. Ja lubię metody obrazowe, wzrokowe,
sam jestem wzrokowcem i wiem, że obraz często lepiej przemawia do ucznia niż wzorki. A ta
"moja" metoda niestety w ogóle nie jest pokazywana w szkołach, dlatego ją prezentuję.
Pozdrawiam.
5 gru 01:09
 ? w 2 a) jest 'usiądą'
? w 2 a) jest 'usiądą'
 Z rysunku:
Niech P(AnB')=P(BnA')=x,
P(AUB)=34 P(AnB)=14. Oblicz P(B), P(A\B)
Z rysunku:
Niech P(AnB')=P(BnA')=x,
P(AUB)=34 P(AnB)=14. Oblicz P(B), P(A\B)
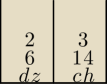 3 W dzudziestosobowej klasie, w której jest 6 dziewczyn, rozlosowano 5 biletów do teatru. Jakie
jest prawdopodobieństwo, że wśród posiadaczy biletów znajdą się dokładnie dwie dziewczyny
Metoda "przegródkowa" − patrz rysunek
3 W dzudziestosobowej klasie, w której jest 6 dziewczyn, rozlosowano 5 biletów do teatru. Jakie
jest prawdopodobieństwo, że wśród posiadaczy biletów znajdą się dokładnie dwie dziewczyny
Metoda "przegródkowa" − patrz rysunek
