Jak wyznacz wzor funkcji g(x)?
FHA: Jak wyznacz wzor funkcji g(x)?
| | 1 | |
Dana jest funkcja f(x)= |
| x3 − 2x2. Funkcja g przyporzadkowuje kazdej liczbie x |
| | 3 | |
wartosc
wspolczynnika kierunkowego stycznej do krzywej f w punkcie x.
1 gru 15:14
Tadeusz:
g(x)=f'(x)=x2−4x
1 gru 15:16
FHA: a skąd sie on wziąl ?
1 gru 15:16
FHA: hmm pochodna funkcji
1 gru 15:17
J:
g(x) = g(f'(x)) = x2 − 4x
1 gru 15:17
FHA: No widzę tutaj pochodna funkcji, na wpadl bym na to aby tutaj pochodną liczyć
1 gru 15:18
J:
..bo f'(x) ... to współczynnik kierunkowy stycznej w punkcie x ...
1 gru 15:18
FHA: a inaczej nie da sie tylko z pochodnej?
1 gru 15:19
FHA: i koncząc zadanie
Zbior wszystkich x, dla ktorych te styczne sa wykresami funkcji malejacych to bedzie
x nalezy do (0,4) ?
1 gru 15:21
Tadeusz:
... a toto co to ?−
1 gru 15:23
FHA: Dana jest funkcja f(x)= ................Funkcja g przyporzadkowuje kazdej liczbie x wartosc
wspolczynnika kierunkowego stycznej do krzywej f w punkcie x. Zbior wszystkich x, dla ktorych
te styczne sa wykresami funkcji malejących to:
g'(x) = x2−4x
więc wychodzi A. (0,4)
1 gru 15:27
Tadeusz:
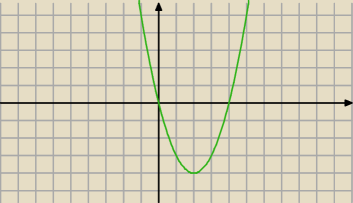
mylisz zbiór w którym funkcja przyjmuje wartości mniejsze od zera ze zbiorem x
dla którego funkcja jest malejąca
1 gru 15:31
FHA: Tadeusz, tak samo w odpowiedz jest
1 gru 15:34
FHA: g(x) <0 ⇒ x ∊ (0,4)
1 gru 15:35
FHA: bo to pochodna
1 gru 15:38
Tadeusz:
problem w tym, że TY nie rozumiesz co piszesz
1 gru 15:42
Mila:
styczna to prosta, y=ax+b, gdzie
a=f'(x0)
1 gru 16:22