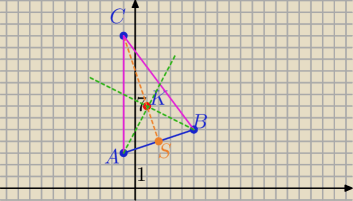
środkowe trójkąta basia06: środkowe trójkąta abc przecinają się w punkcie k(1,7). wyznacz współrzędne wierzchołka c, jeśli wiadomo, że a(−1,3) i (wektor)AB=[6,2]

Mila: K=(1,7) A(−1,3)→T_[6,2]=B(−1+6,3+2)=(5,5) środkowe przecinają w punkcie, który je dzieli w stosunku 2:1. S=(2,4) środek AB SC^→=2*SK^→=2*[−1,3]=[−2,6] K=(1,7)→T_[−2,6]=C(−1,13)

Bogdan: Można skorzystać z zależności:

	xA + xB + xC		yA + yB + yC
xs =		, ys =
	3		3

S = (x_S, y_S) to środek ciężkości trójkata Obliczamy współrzędne punktu B: B = (−1 + 6, 3 + 2) = (5, 5), Oznaczamy C = (x_c, y_c)

	−1 + 5 + xc
1 =		⇒ xc = −1
	3

	3 + 5 + yc
7 =		⇒ yc = 13
	3