Rachunek prawdopodobieństwa Johny: Wiadomo, że P(B')=¹₄, P(AuB)=¹⁵₁₆, P(AnB)=¹₁₆ Oblicz : P(A\B) P(A'nB') Prosiłbym o same wyniki, rozwiązałem sam i chciałbym porównać.

Eta:

	3		1
P(A\B)=		, P(A'∩ B')=
	16		16

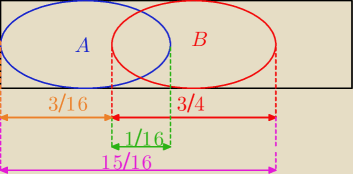Gustlik: Ja mam świetny graficzny sposób na takie zadania, niemal bez wzorów, liczę z rysunku jak powyżej:

	1		3
P(B')=		, ⇔ P(B)=
	4		4

P(AuB)={15}{16},

	1
P(AnB)=		Oblicz : P(A\B) P(A'nB')
	16

	15		3		15		12		3
P(A\B)=		−		=		−		=
	16		4		16		16		16

Korzystam z praw de Morgana:

	15		1
P(A'nB')=P(AUB)'=1−P(AUB)=1−		=
	16		16