rozwiąż nierówność basia06: rozwiąż |2x−8| < |x |+ |x+4| oblicz sumę jej całkowitych rozwiązań mniejszych od 15

basia06: proszę o pomoc...

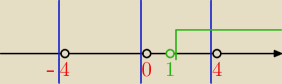
Bogdan: 2|x − 4| < |x| + |x + 4| x = 4, x = 0, x = −4 dla x∊(−∞, −4): −2x + 8 < −x − x − 4 sprzecczność dla x∊<−4, 0): −2x + 8 < −x + x + 4 ⇒ 2x > 4 ⇒ x > 2 sprzeczność dla x∊<0, 4): −2x + 8 < x + x + 4 ⇒ 4x > 4 ⇒ x > 1, x∊ (1, 4) dla x∊<4, +∞): 2x − 8 < x + x + 4 ⇒ −8 < 4 ⇒ x∊<4, +∞) Odp.: x∊(1, +∞)

Metis: |2x−8|<|x|+|x+4| |x|+|x+4|−|2x−8|>0 Rozwiązuje w przedziałach: 1) x∊(−∞, −4) 2)x∊[−4,0) 3)x∊[0,4) 4)x∊[4,+∞) Ad.1 −x−x−4+2x−8>0 Brak rozwiązania. Ad.2 x−x−4+2x−8>0 2x−12>0 x>6 x∊(6,+∞) Nie zawiera sie w przedziale. Ad.3 x+x+4+2x−8>0 4 x−4>0 x>1 x∊(1,+∞) Łączymy przedział , zatem: x∊(1,4) Ad.4 x+x+4−2x+8>0 12>0 x∊[4,+∞) Ostateczna odpowiedź: x∊(1,+∞) x>1 Teraz szukamy całkowitych rozwiązań, stąd: x∊(2,3,4,5,6,7,8,9,10,11,12,13,14) Zsumuj...