Nierówność z pierwiastkiem. Metis: Jak nie pogubić się w łączeniu przedziałów? Mam taka nierówność: √x−2 <8−x Jeśli 8−x <0 ⇔ x>8 to nierówność jest sprzeczna, na podstawie własności pierwiastka kwadratowego. Rozważmy przypadek, gdy 8−x>0 ⇔ x<8 Jeśli x<8 oraz x−2≥0⇔ x≥2, prawidłowym jest obustronne podnoszenie do kwadratu, w wyniku którego otrzymujemy: x−2<x²−16x+64 x²−17x+66>0 x₁=6 v x₂=11 x∊(−∞,6) U (11,+∞) I teraz przychodzi moment podania ostatecznej odpowiedzi , z której podaniem mam czasami problemy: ▯x<8 ▯x≥2 ▯x∊(−∞,6) U (11,+∞) Jaka będzie ostateczna odpowiedź ?

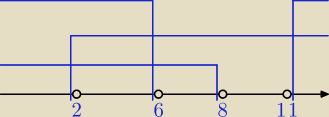
Bogdan: x∊<2, 6)