narysuj wykres funkcji y=f(x) i y=g(x) a następnieznajdż współrzędneprzecięcia t biedny żuczek z matmy: mam zadanie do rozwiązania...uczyłam się matematyki bardzo dawno temu ,potrzebuje pomocy... narysuj wykres funkcji y=f(x) i y=g(x) a następnieznajdż współrzędneprzecięcia tych wykresów f(x) = x+2 x g(x) = 2x+3

Janek191:

	x + 2
f(x) =		?
	x

biedny żuczek z matmy: tak

biedny żuczek z matmy: czy możesz mi rozwiązać krok po kroku?

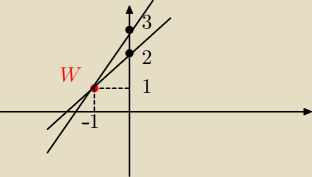
Krystek: 2x+3=x+2⇒x=−1 i y=1 W(−1,1)

Krystek: O to zmienia postać!

biedny żuczek z matmy: dasz radę ?

Tadeusz:

biedny żuczek z matmy: nie rozumiem

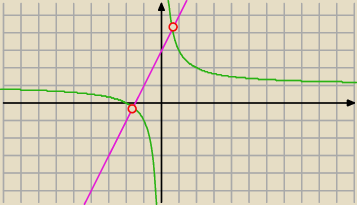
Tadeusz: x≠0 x+2=2x²+3x ⇒ 2x²+2x−2=0 ⇒ x²+x−1=0

	−1−√5		−1+√5
Δ=5 x1=		x2=
	2		2

y₁=? y₂= ?

Tadeusz:

	x+2		2
g(x)=		=1+		... to funkcja wymierna ... jej wykresem jest hiperbola (na zielono)
	x		x

f(x)=2x+3 ... to funkcja liniowa ... jej wykres to prosta (fiolecik)

biedny żuczek z matmy: a krok po kroku?

biedny żuczek z matmy: super już lepiej a f(x)=2x+3 jak z tym rozwiązaniem...? ja poprostu muszę wiedzieć dokładnie co skąd się bierze ....sorry ale tylko w ten sposób zrozumiem

biedny żuczek z matmy: skąt ty znalazłes ten 3x?

biedny żuczek z matmy: skąd?

Tadeusz: ... punkty przecięcia to punkty wspólne ... należące do obu funkcji

	x+2
zatem		=2x+3 ⇒ x+2=x(2x+3) itd−
	x

biedny żuczek z matmy: napisz prosze cyfry jakie zaznaczyłeś na wykresie?

biedny żuczek z matmy: wyliczyłes deltę wzór który znam tj Δ = bkwadrat − 4ac...jak ci wyszło 5 i −1

biedny żuczek z matmy: x1 = −b+pierw z Δ x2= −b−pierw zΔ

undefined: Tak jak napisali powyżej po prostu sprawdzasz kiedy f(x) = g(x) x+2 = x(2x+3) x + 2 = 2x² + 3x 2x² +2x − 2 = 0 x² +x − 1 = 0 Δ= 1² − 4(−1) =1+4 = 5

	−1−√5
x1 =
	2

	−1+√5
x2 =
	2

undefined: teraz podstaw x₁ x₂ do którejś z funkcji i oblicz prosto y₁ y₂

biedny żuczek z matmy: ah ok...rozumiem...dzięki