proszę o rozwiązanie Michał: Spośród wszystkich prostokątów symetrycznych względem osi y , których dwa wierzchołki należą do wykresu funkcji f(x) = − x² + 4 a dwa do osi x , wyznacz wierzchołki prostokąta o największym polu . Oblicz pole tego prostokąta

	2		2		2		8
wyniki to A = ( −		, 0 ) B = (		,0) C =(		,		)
	√3		√3		√3		3

	2		8
D = ( −		,		)
	√3		3

	32
P =		√3
	9

zupełnie nie wiem jak się do tego zabrać ( narysowałem tylko wykres )

Michał:

	x		x
zacząłem tak I ABI = x A = ( −		; 0 ) B= (		; 0 ) A i B to wierzchołki
	2		2

prostokąta gdzie x ∊( 0,4)

	x		x2		x		x2
D = ( −		; −		+ 4 ) C = (		; −		+ 4 )
	2		4		2		4

	x2
PABCD = x * ( −		+ 4 )
	4

nie wiem czy dobrze

3Silnia&6: wierzcholki A(−x,0) ,B(x,0), C(−x,−x²+4), D(x,−x²+4) P = |AB| * |BC| P = (x − (−x)) * (−x² + 4 ) = 2x * (−x² + 4) = −2x³ + 8x f(x) = −2x³ + 8x f'(x) = −6x² + 8

	4
f'(x) = 0 ⇔ 6x2 = 8 ⇔ x2 =
	3

	2		−2
x =		v x
	√3		√3

	−2
A(		,0), B...
	√3

Michał:

	x
dziękuję bardzo liczyłem pochodną ale chyba nie można dać		za pierwszą współrzędną
	2

punktu

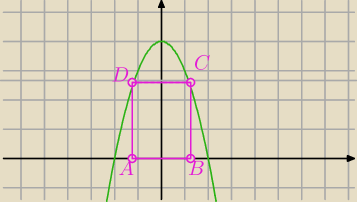Tadeusz: A=(−x_B,0) B=(x_B,0) C=(x_B,−x_B²+4) D=(−x_B,−x_B²+4) |AB|=2x_B |BC|=−x_B²+4 P=2x_B(−x_B²+4) P'=2(−x_B²+4)−4x_B²=−6x_B²+8

	2√3
P'=0 ⇒ w warunkach zadania xB=		... itd −
	3

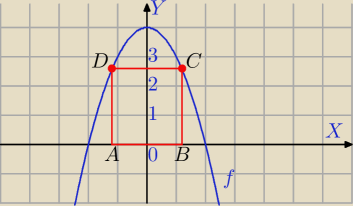Mila: f(x)=−x²+4 Miejsca zerowe : x=2, x=−2 A(x_A,0), B(x_B,0) dla x_B>0 w związku z symetrią względem OY mamy: x_A=−x_B ⇔|AB|=2x_B C=(x_B,−x_B²+4) |BC|=|−x_B²+4| rozważymy przypadek : 0<x_B<2 wtedy mozemy zapisać : |BC|=−x_B²+4 P_ABCD|=|AB|*|BC|⇔P(x_B)=2x_B*(−x_B²+4)⇔ P(x_B)=−2x_B³+8x_B P'(x_B)=−6x_B²+8 badamy kiedy pochodna równa 0.

	4
−6xB2+8 =0⇔xB2=		i xB>0 ( tak założyliśmy)
	3

	2		2		2
xB=		i P'(xB)>0 dla x∊(−		,		)⇔pochodna przy przejsciu
	√3		√3		√3

	2
przez punkt (		,0) zmienia znak z dodatniego na ujemny⇔
	√3

	2
dla x=		pole prostokąta jest największe.
	√3

	2		2
A=(−		,0) , B=(		,0)
	√3		√3

	2		4		2
C=(		,−		+4)=(		, 223)
	√3		3		√3

	2
D=(−		, 223)
	√3

	2		4√3
|AB|=2*		=
	√3		3

	8
|BC|=
	3

==========

	4√3		8
P=		*
	3		3

	32√3
P=
	9

===========