zadanko Blue: Funkcja f jest określona wzorem f (x) =| x −1| − x −m dla wszystkich liczb rzeczywistych x. Wyznacz wszystkie wartości parametru m, dla których funkcja f ma tylko jedno miejsce zerowe. Mam schemat rozwiązania do tego zadania, ale go kompletnie nie rozumiem może ktoś by mi to wytłumaczył

Blue: Cofam pytanie, już rozumiem

Saizou : obliczmy miejsce zerowe lx−1l−x−m=0 1) dla x<1 −x+1−x−m=0 −2x=m−1

	1−m
x=
	2

2) dla x≥1 x−1−x−m=0 m=−1 czyli dla tej wartości m, nie ma miejsc zerowych wróćmy do przypadku 1)

	1−m
x=		i x<0
	2

1−m
	<0
2

1−m<0 1<m

Saizou : eh... błąd miało byc x<1 czyli

1−m
	<1
2

Tadeusz: ... a dobrze zapisałaś treść ?

Blue: Tadeusz, nawet nie zapisywałam , bo skopiowałam, Saizou Twoje rozwiązanie lepsze, w kluczu jakieś dziwne jest xd

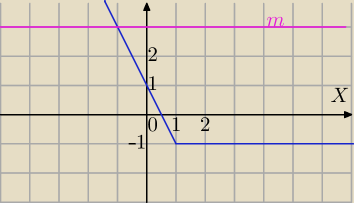Mila: f(x)=|x−1|−x−m g(x)=|x−1|−x g(x)=m⇔g(x)−m=0⇔f(x)=0 1) m>−1 jedno miejsce zerowe 2) m=−1 i x≥1 f(x)=x−1−x+1=0 ⇔ f(x) ma nieskończenie wiele miejsc zerowych, każda liczba x≥1 jest miejscem zerowym f(x) dla m=−1 3) m<−1 brak miejsc