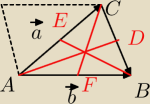
wektory kyrtap: Proszę o spr zadania Trójkąt jest rozpięty na wektorach a,b . Wyrazić środkowe przez,a,b. Z zasady równoległoboku mam Nie będę pisał znaku → ale będzie mi chodziło o wektory: BC + b = a BC= a−b CD + AD = AC ⇒ AD = AC − CD

	1		1		1		1		1
AD = a −		(a−b) = a −		a +		b =		a +		b
	2		2		2		2		2

AE + EB = AB ⇒ EB = AB −AE

	1
EB = b −		a
	2

CF + AF = AC CF = AC − AF

	1
CF = a −		b wszędzie korzystałem z zasady równoległoboku ale na stronce zadania info
	2

inaczej jest proszę o wytłumaczenie dlaczego tak jeśli jest błąd

PW: (1) AD^→ = b^→+ BD^→, a ponieważ jest to środkowa, mamy

	1
(2) BD→=		BC→.
	2

Z kolei b^→+ BC^→= a^→, skąd (3) BC^→ = a^→− b^→. Podstawienie (3) do (2) i (2) do (1) daje

	1
AD→ = b→+		(a→−b→)
	2

	1
AD→ =		(a→+ b→).
	2

Taki wynik staje się oczywisty, gdy połączyć końce środkowych i zobaczyć powstałe równoległoboki.

kyrtap: a jak z tymi wektorami EB i CF

kyrtap:

PW: Nic nie trzeba liczyć, mówi się o takiej sytuacji "mutatis mutandis" − wystarczy zamienić wektory nazwami, a rozumowanie zostaje bez zmian, wyniki muszą być te same − "wektor środkowa" jest połową sumy dwóch odpowiednich "wektorów boków". Po uwzględnieniu (3) i tego, że BA^→= − b^→ wyrazimy bez liczenia BE^→ jako połowę sumy ...

kyrtap: czyli co źle wyznaczyłem

kyrtap:

kyrtap:

Mila: Aby wyznaczyć CF^→ w zależności od a^→ i b^→, możesz rozumować tak: Aby przejść z punku C do Punktu F możesz iść od C do A, potem od A do F co zapiszemy:

	1		1
CF→=−a→+		b→=		b→−a→
	2		2

Analogiczne rozumowanie do wyznaczenia BE^→

	1
BE→=−b→+		a→
	2

kyrtap: czyli mój sposób jest błędny?

Mila: Masz tam błędy, przeczytaj dokładnie co Ci napisałam, to praktyczny sposób.

kyrtap: dobrze tylko nie wiem czemu reguła równoległoboku tutaj się nie spr

Mila: Sprawdza się, ale trzeba dobrze stosować.

kyrtap: Mila myślę że dobrze zastosowałem