Dwa zadania z matury rozszerzonej. trq: Dwa zadania z matury rozszerzonej, które nie wiem jak tknąć:

	|CE|
1. W trójkącie ABC poprowadzono środkową CD i wyznaczono na niej taki punkt E, że
	|ED|

	1
=		. Prosta przechodząca przez punkty AE przecina bok BC w punkcie P. Wykaż, że
	3

	|CP|		1
		=
	|PB|		6

2. Oblicz ile jest liczb naturalnych sześciocyfrowych, w których zapisie występują dokładnie dwie dwójki i jedna jedynka.

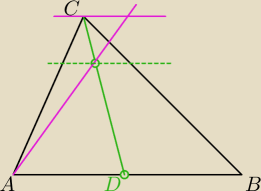
Tadeusz: ... i wszystko jasne

Tadeusz: ... "kuma" żabka ? −

trq: Szczerze to średnio. Miało być coś w stronę twierdzenia Talesa?

Mila: 2) {0,1,2,3,4,5,6,7,8,9} zbiór cyfr 1) 2|21XXX dwójka na pierwszej pozycji

5 1		4 1
	*		*83 −wybór miejsca dla dwójki, wybór miejsca dla jedynki, na pozostałe 3

miejsca ciągi 3 wyrazowe z elementów {0,3,4,5,6,7,8,9} 2) 1|22XXX jedynka na pierwszej pozycji

5 2
	*83 wybór dwóch miejsc dla dwóch dwójek, na pozostałe 3 miejsca ciągi 3 wyrazowe z

elementów {0,3,4,5,6,7,8,9} 3) X221XX na pierwszej pozycji jedna z liczb {3,4,5,6,7,8,9}

	5 2		3 1
7*		*		*82

Razem: 5*4*8³+10*8³+7*10*3*8²=28 800 sprawdź rachunki

Tadeusz:

|CN|
	=...
|AD|

|CN|
	=...
|AB|

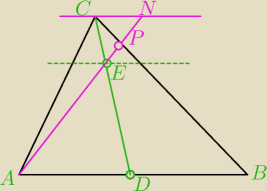
a skoro tak to

|CP|
	=1/6
|PB|

trq : Okej, drugie zadanie załapałem. Gorzej z tym pierwszym z którego mało co rozumiem :f

Tadeusz: ... to pierwsze jest banalne ... Trójkąty ADE i CEN są podobne. Znasz też ich skalę podobieństwa.

	|CE|		1		|CN|		1
Skoro		=		to i		=
	|ED|		3		|AD|		3

|AB|=2*|AD| zatem:

|CN|		1
	=
|AB|		6

Trójkąty PCN i ABP są podobne ich skala podobieństwa to 1/6

	|CP|		1
zatem i		=
	|PB|		6

undefined: wszystko jest banalne tylko jak można pamiętać o rzeczach które były 2 lata temu :C Biorę się za powtórkę.

Tadeusz: ... a ja je miałem 45 lat temu ...

undefined: W takim przypadku musisz być profesorem

trq: Okej, dziękuję @Tadeusz. Rozumiem wszystko tylko nie rozumiem jak na to wpaść samemu . Co do tego zadania drugiego mam jeszcze takie czysto techniczne pytanie, właściwie elementarne. Dlaczego przy wyborze miejsca dla dwójki lub jedynki szukamy go kombinacjami, a resztę liczymy wariacjami?

Mila: Na pozostałych miejscach mogą być ciągi z powtórzeniami.

trq: Okej, to mniej więcej łapię. Po prostu nie zawsze widzę tą różnicę pomiędzy ciągiem a kombinacją, stąd to pytanie. Dziękuję ślicznie

Tadeusz: undefined ...rozczaruję Cię ... jestem meblarzem −

Metis: Marnujesz się

Tadeusz: ... niby dlaczego?

Metis: Miałem na myśli fakt, że dobrze rozumiesz matematykę

Tadeusz: ... dobra jest na powstrzymanie sklerozy i stetryczenie −

Metis:

trq: Kurde no nie rozumiem tego drugiego zadania :<. To znaczy wiem co z czego się wzięło w tym roziwązaniu, ale czemu tak a nie inaczej?

Mila: Miałeś już rachunek prawdopodobieństwa?

Lukas: A ja tylko jednego zadania nie zrobiłem z R

Mila: Chodzi Ci o "pozostałe 3 miejsca"?

Lukas: Mila masz jakieś zadania żeby dobrze opanować f.kwadratową ? myślisz, że to co jest na zadania info wystarczy jak wszsytko przerobię ?

Mila: Wystarczy, tam są zadania dość trudne. Przeglądaj stare maturki pod tym kątem.

razor: pazdro + kiełbasa + zadania.info i dobrze opanujesz każdy dział (ew. wybierz tylko 2 zbiory jeśli nie masz tyle czasu)

Lukas: razor a samo zadania.info nie wystarczy ?

trq: Właśnie teraz się męczę z prawdopodobieństwem. Niby jak czytam Twoje rozwiązanie to rozumiem co i jak, ale sam bym po prostu chyba na to nie wpadł. Nie do końca czuję kiedy użyć wariacji, a kiedy kombinacji.

daras: spróbujcie zadań z Gdowskiego i śp. Plucińskiego

Mila: Musisz poczytać dokładnie teorię i przykłady w podręczniku.

undefined: @trg jeżeli np. idziesz pograć na orlika z kolegami jest was 10, a jedną drużynę tworzy 5. Ile

	10 5
można wybrać różnych drużyn?

Na ile sposobów możecie się ustawić na boisku. (bramkarz, dwóch obrońców i dwóch napastników) 5! Jeżeli mamy kolegę, który stoi tylko na bramce to możemy się ustawić na 4! sposobów. Myślę, że to trochę rozjaśni

undefined: Ilość wszystkich możliwych ustawień na boisku (10 zawodników i pięć pozycji{1,2,3,4,5})

	10 5
5! *