a ma: Wykazać , że dla dowolnych zbiorów A,B,C prawdziwa jest równość: (A − B) ∩ C = (A ∩ C) − B Pomoże ktoś ?

Saizou : x∊(A\B)∩C⇔x∊A\B i x∊C⇔x∊A i ¬x∊B i x∊C⇔x∊A i x∊C i ¬x∊B⇔x∊A∩B i ¬x∊C⇔x∊(A∩C)\B

ma: a mógłby ktoś to rozpisać jaśniej albo jakoś wytłumaczyć Bo jak wiem co oznaczają poszczegolne symbole ale nie rozumiem tego rozwiązania wcale. Jak takie zadania robić ?

ma: ?

Saizou : Korzystasz z definicji A\B oraz D∩C

ma: nie mam pojęcia jak to wykorzystać. Takiego zadania to dla mnie koszmar.

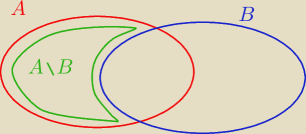
Saizou : więc jeśli x∊A\B to x∊A i x∉B no ale ∉ to inaczej ~∊ analogicznie z przekrojem

ma: na rysunku to ja wiedziałem jak to wygląda ale nie umiem tego udowodnić.

Gray: Przepiszę, bo Saizou pod koniec odrobinę pomieszał, ale nic odkrywczego nie napiszę: x∊(A\B)∩C⇔(x∊A\B) ⋀ x∊C⇔(x∊A ⋀ x∉B) ⋀ x∊C⇔(x∊A ⋀ x∊C) ⋀ x∉B ⇔x∊A∩C ⋀ x∉B⇔x∊(A∩C)\B

ma: jednak na swoim rysunku miałem inaczej, gdzie wstawiłeś zbiór C ?

ma: chyba bym musiał się tego nauczyć na pamięć, bo nie rozumiem

Saizou : faktycznie Gary ale koniunkcja jest przemienna p∧q⇔q∧p i dla większej ilości też to działa

ma: nie można tego jakoś prościej zapisać?

Gray: Saizou, nie o koniunkcję się rozchodzi, a o to: "x∊A∩B i ¬x∊C"