bryły obrotowe nope:

	1
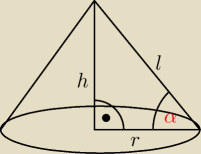
1. Tangens kąta nachylenia tworzącej stożka do płaszczyzny jest równy 1		. Niech Pb
	3

oznacza pole powierzchni bocznej, zaś Pc − pole powierzchni całkowitej tego stożka. Wówczas:

	4
A. Pc=2Pb B. Pc=1,5Pb C. Pc=		Pb D. Pc=1,6Pb
	3

2. Wysokość stożka jest równa √44, a promień podstawy − 10. Jaką miarę ma kąt środkowy wycinka koła tworzącego powierzchnię boczną stożka? 3. Jedna kula ma objętość 27 razy większą od drugiej. Jaki jest stosunek obwodu wielkiego koła dużej kuli do obwodu wielkiego koła małej kuli. (+ bardzo proszę o obliczenia)

3Silnia&6:

	4
tg α =
	3

h		4
	=
r		3

	4r
h =
	3

h² + r² = l²

	4r
(		)2 + r2 = l2
	3

16r2
	+ r2 = l2
9

25r2
	= l2 /√
9

5r
	= l
3

	5r		5r2π
Pb = πrl = πr*		=
	3		3

	5r2π		8r2π
Pc = Pb + Pp =		+ πr2 =
	3		3

P_c = 8/5 P_b = 1,6P_b ( odp. D)

x: h = √44 , r = 10 l² = h² + r² ⇒ l = 12 Pw = Pb Pb = πrl = 120π

	α		α		5		α
Pw =		πl2 120π =		π144 | :144π		=
	360°		360°		6		360°

α = 300°

3Silnia&6:

V1		(R1)3
	=		= 27 ⇔ R1 = 3R2
V2		(R2)3

P1		(R1)2
	=
P2		(R2)2

nope: dzięki bardzo