wykres funkcji z logarytmem
Sylwia: Proszę o pomoc, czy ktoś mógłby by mi pomóc narysować krok po kroku z odpowiednimi
przekształceniami pewien wykres? Chciałabym żeby to było z objaśnieniami, bo gotowy wykres
nic mi nie da, mogłabym go sobie w geogebrze narysować a zależy mi żeby w końcu się tego
nauczyć.
Wykres funkcji wygląda tak:
y= −|log2|x−3||+1
ten logarytm jest u podstawy z 2

z góry bardzo serdecznie dziękuję!
27 lis 16:28
razor: y1 = log2x
y2 = log2|x| − symetria częściowa względem osi OY
y3 = log2|x−3| − przesunięcie o wektor [3,0]
y4 = |log2|x−3|| − symetria częściowa względem osi OX
y5 = −|log2|x−3|| − symetria względem osi OX
y6 = −|log2|x−3||+1 − przesunięcie o wektor [0,1]
27 lis 16:39
razor:
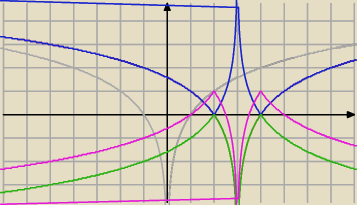
27 lis 16:41
razor: na różowo końcowy wykres
27 lis 16:41
Sylwia: a czy to ma jakieś znaczenie czy najpierw zrobię funkcję y5 czy y6? pewnie tak, ale dlaczego?
27 lis 16:42
Sylwia: o rany boskie..

27 lis 16:45
Sylwia: jak to wszystko sie podziało
27 lis 16:45
razor: zauważ że przekształcenie
y
4 = |log
2|x−3||
y
5 = −|log
2|x−3||
y
6 = −|log
2|x−3|| + 1
oraz
y
4 = |log
2|x−3||
y
5 = |log
2|x−3|| + 1
y
6 = −|log
2|x−3|| − 1
nie dają tego samego wyniku

jeśli najpierw chcesz przesuwać o wektor, a później zrobić symetrie to może to wyglądać tak
y
4 = |log
2|x−3||
y
5 = |log
2|x−3|| − 1 − przesunięcie o wektor [0,−1]
y
6 = −|log
2|x−3|| + 1 − symetria
27 lis 16:45
Sylwia: oczywiście bardzo dziękuję za pomoc <3
27 lis 16:45
Sylwia: w sumie jako jeszcze niedoświadczona licealistka, skąd mam wiedzieć co wykonywać pierwsze?

27 lis 16:46
razor: jak sobie wejdziesz w opcję rysowania... to kolejne kolorki to kolejne przekształcenia (czarny
− y1, szary − y2 itd.)
27 lis 16:46
razor: nie ma jakichś uniwersalnych zasad co do przekształcania, musisz po prostu spróbować samej
porobić odpowiednią ilość przykładów, wtedy będzie to widać od razu

27 lis 16:47
razor: mogę po kolei narysować każde przekształcenie oddzielnie ale nie chcę spamować

daj znać
jeśli tego potrzebujesz
27 lis 16:48
Sylwia: taaak, jeśli byłbyś taki miły z chęcią poproszę o każde przekształcenie oddzielnie
27 lis 16:50
razor:
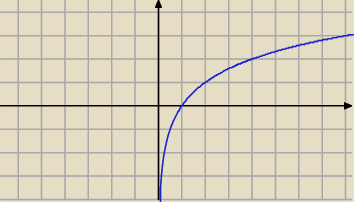
y
1 = log
2x
27 lis 16:53
razor:
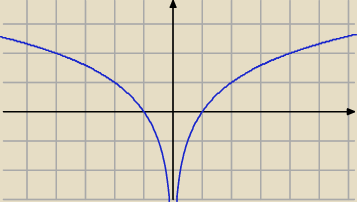
y
2 = log
2|x|
27 lis 16:53
razor:
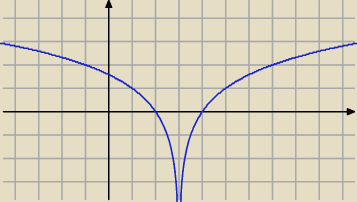
y
3 = log
2|x−3|
27 lis 16:54
razor:
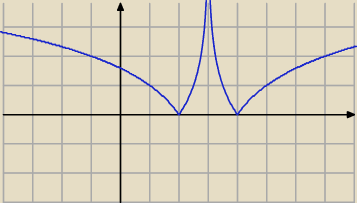
y
4 = |log(|x−3|)/log(2)|
27 lis 16:54
razor: y
4 = |log
2|x−3|| miało być

27 lis 16:55
razor:
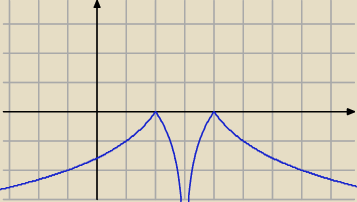
y
5 = −|log
2|x−3||
27 lis 16:56
razor:
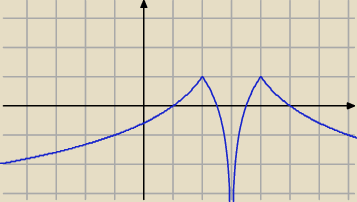
y
6 = −|log
2|x−3||+1
27 lis 16:56
Sylwia: jesteś niesamowity

chciałbyś mi może pomóc z drugą częscią tego zadania?
27 lis 16:58
razor: hmm?

27 lis 16:58
Sylwia: albo chociaż, pomęczę sie z tym sama, jeżeli nie dam rady na pewno znowu tu uderzę ;>
27 lis 16:59
Sylwia: ahh mam pytanko
27 lis 17:41
Sylwia: muszę wyznacyzć liczbę rozwiązań tego równania w zależności od m. Jeżeli ta funkcja równałaby
się m, to jak mam stwierdzić gdzie równanie ma dwa rozwiązania a gdzie już cztery, obliczyć
jakąś asymptotę poziomą?
27 lis 17:42
Sylwia: halo misie? :C
27 lis 18:06
Sylwia: a moze teraz ktoś?
27 lis 19:57
 z góry bardzo serdecznie dziękuję!
z góry bardzo serdecznie dziękuję!


 jeśli najpierw chcesz przesuwać o wektor, a później zrobić symetrie to może to wyglądać tak
y4 = |log2|x−3||
y5 = |log2|x−3|| − 1 − przesunięcie o wektor [0,−1]
y6 = −|log2|x−3|| + 1 − symetria
jeśli najpierw chcesz przesuwać o wektor, a później zrobić symetrie to może to wyglądać tak
y4 = |log2|x−3||
y5 = |log2|x−3|| − 1 − przesunięcie o wektor [0,−1]
y6 = −|log2|x−3|| + 1 − symetria


 daj znać
jeśli tego potrzebujesz
daj znać
jeśli tego potrzebujesz
 y1 = log2x
y1 = log2x
 y2 = log2|x|
y2 = log2|x|
 y3 = log2|x−3|
y3 = log2|x−3|
 y4 = |log(|x−3|)/log(2)|
y4 = |log(|x−3|)/log(2)|

 y5 = −|log2|x−3||
y5 = −|log2|x−3||
 y6 = −|log2|x−3||+1
y6 = −|log2|x−3||+1
 chciałbyś mi może pomóc z drugą częscią tego zadania?
chciałbyś mi może pomóc z drugą częscią tego zadania?
