Pomocy !!
Jola: Hej, Czy podjąłby się ktoś z was rozwiązania trzech zadań z geometrii na poziomie matury
rozszerzonej ? Jeśli tak to proszę o informację na adres Palka220@interia.pl
27 lis 09:15
Tadeusz:
... wklepuj te zadania tutaj
aha ... i chyba ty nie masz maila ... nie umiesz nawet napisać adresu −

27 lis 12:30
PW: palka/sub>220
27 lis 14:51
PW: Przepraszam, próbowałem i za wcześnie kliknąłem. Napisanie "podkreślnika" w tym edytorze to
wyzwanie, ponieważ został on zarezerwowany jako znak sterujący − powoduje, że następny po nim
znak (lub grupa znaków ujęta w nawiasy "{}" jest traktowany jako indeks dolny.
palka–220@interia.pl
wymagało napisania "__ Alt0150"
27 lis 14:57
Jola: Tak chodzi o ten adres co napisał PW, każdemu zdarza się pomylić po prostu nie zwróciłam
uwagi,to nie powód by od razu mówić że ktoś czegoś nie potrafi

27 lis 16:27
Mila:
Pisz tu swoje zadania.
27 lis 16:37
Jola: Zadanie 1
Kąt przy wierzchołku trójkąta równoramiennego jest równy α. Wyznaczyć stosunek promienia
okręgu opisanego na trójkącie do promienia okręgu wpisanego w ten trójkąt.
Zadanie 2
W stożek wpisano walec o wysokości równej średnicy podstawy stożka. Znaleźć stosunek
| | P1 | |
|
| pola całkowitej powierzchni walca do pola podstawy stożka wiedząc, że kąt zawarty |
| | P2 | |
między osią a tworzącą stożka jest równy α.
Zadanie 3
Dany jest sześcian ABCDA
1B
1C
1D
1 o krawędzi a. Niech M i N będą odpowiednio środkami
| | a | |
krawędzi AA1 i CC1. Na przedłużeniu krawędzi DD1 obrano punkt P taki, że D1P= |
| . |
| | 2 | |
Przez punkty M,N i P poprowadzono płaszczyznę. Znaleźć pole przekroju sześcianu tą
płaszczyzną.
27 lis 20:15
Jola: Jeśli ktoś mógł mi pomóc w tych zadaniach bardzo proszę

27 lis 20:15
===:
... toś się
Mila narobiła −

| | R | |
Pisałem Jej kilka dni temu, że najłatwiej wprost |
| |
| | r | |
27 lis 21:21
===:
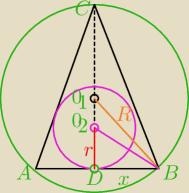
|BD|=x
27 lis 21:32
27 lis 21:35
Jola: Dziękuję bardzo ślicznie, a może wiecie jak dwa pozostałe zacząć bo to właśnie jest gorsza
rzecz bo nawet nie wiem jak zacząć je
27 lis 21:42
Mila:
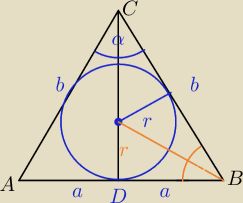
1)
|AB|=2a,|AC|=|BC|=b
r− promień okręgu wpisanego w ΔABC
R− promień okręgu opisanego na ΔABC
a=R sinα
===========================
27 lis 21:48
Mila:
21:48 masz II sposób.
Może kolega poda z mniejszą liczbą obliczeń.
27 lis 21:50
Mila:
Jolu masz może odpowiedzi, bo nie chce mi się sprawdzać rachunków.
27 lis 21:52
===:
... przecież podałem −

a kąty ... niech dojdzie sama
27 lis 21:54
===:
...Milu .... Twój wynik z 21:48 i mój są identyczne
27 lis 22:02
Jola: do pierwszego w odpowiedziach mam odp :
27 lis 22:17
Tadeusz:
...to to samo −

27 lis 22:20
Jola: no to dobrze, jestem wam bardzo wdzięczna

a wiecie może jak zrobić 2 i 3 ?
27 lis 22:26
Mila:
Napisz odpowiedzi.
27 lis 22:34
Jola: W drugim mam odpowiedź:
27 lis 22:39
Jola: W zadaniu 3 mam napisane tylko:
i nic więcej prócz tego nie ma ..
27 lis 22:53
Jola: W zadaniu 3 mam napisane tylko:
27 lis 23:00
Jola: No jak byś mogła to poszukaj błędu, jestem Ci bardzo wdzięczna za pomoc tak dokładną

27 lis 23:01
Mila:

R− promień podstawy stożka
r− promień podstawy walca
h=2R− wysokość walca
Pc.walca=2πr
2+2πr*2R=2π*r(r+2R)
Pps=πR
2
W ΔBFE:
2Rtgα=R−r
r=R−2Rtgα
| | 1 | |
r=R(1−2tgα), r>0 ,tgα< |
| |
| | 2 | |
| Pc.walca | | 2π*r(r+2R) | |
| = |
| = |
| Pps | | πR2 | |
| | 2*R(1−2tgα)*(R(1−2tgα)+2R) | | 2R*R*(1−2tgα)*(1−2tgα+2) | |
= |
| = |
| = |
| | r2 | | R2 | |
=2*(1−2tgα)(3−2tgα)
===============
27 lis 23:09
Jola: dziękuję ślicznie, a pomożesz jeszcze z trzecim ?

27 lis 23:15
Mila:
Tak.
27 lis 23:19
Tadeusz:
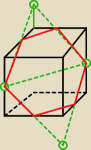
3) jest banalne
| | a√2 | |
w przekroju otrzymasz sześciokąt foremny o boku b= |
| |
| | 2 | |
Zatem pole tego sześciokąta
| | 3√3b2 | | 3√3a2 | |
P= |
| = |
| ... coś nie tak albo już śpię −  |
| | 2 | | 4 | |
27 lis 23:23
Jola: Ale w odpowiedziach jest trochę inaczej oczywiście książka może się mylić jak najbardziej,a
Mila Ty jak sądzisz co do tego zadania 3 ?

27 lis 23:38
Tadeusz:
27 lis 23:44
Mila:
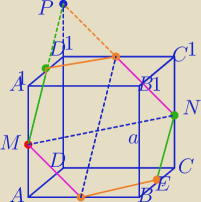
Tu masz wyjaśnione jak rysować taki przekrój.
http://www.zadania.info/d454/7037217
|MN|=a
√2
Powstał sześciokąt foremny
| | a | |
Oblicz pole sześciokata foremnego o boku równym b= |
| √2 |
| | 2 | |
dokończ, ale to będzie inna odp.
Może ten przekrój inaczej wygląda?
Jutro pomyslę..
28 lis 00:07
Tadeusz:
√3zgubiłaś w ostatnim wzorze −

28 lis 00:10
Tadeusz:
... i wynik taki jak u mnie ... czyli masz błąd w odpowiedziach
28 lis 00:13
Mila:
Tak , zgubiłam
√3 , późna pora i też zasypiam.
Tadeusz, jeszcze trzeba wykazać, że to sześciokąt foremny, mam na myśli, że cięcia
krawędzi są w środkach.
Dobranoc.

28 lis 00:17
Jola: Dziękuję za pomoc, ale jeśli byście mogli sprawdzić te 3 czy na pewno to taki przekrój byłabym
wdzięczna

28 lis 12:03
Tadeusz:
... NIE ULEGA NAJMNIEJSZEJ WĄTPLIWOŚCI
28 lis 12:21
Jola: A w zadaniu 2 tam w przed ostatnim równaniu w mianowniku nie powinno być R2 zamiast r2 ?
28 lis 13:14
Tadeusz:
powinno
28 lis 14:24




 |BD|=x
|BD|=x
 1)
|AB|=2a,|AC|=|BC|=b
r− promień okręgu wpisanego w ΔABC
R− promień okręgu opisanego na ΔABC
1)
|AB|=2a,|AC|=|BC|=b
r− promień okręgu wpisanego w ΔABC
R− promień okręgu opisanego na ΔABC
 a kąty ... niech dojdzie sama
a kąty ... niech dojdzie sama

 a wiecie może jak zrobić 2 i 3 ?
a wiecie może jak zrobić 2 i 3 ?

 R− promień podstawy stożka
r− promień podstawy walca
h=2R− wysokość walca
Pc.walca=2πr2+2πr*2R=2π*r(r+2R)
Pps=πR2
W ΔBFE:
R− promień podstawy stożka
r− promień podstawy walca
h=2R− wysokość walca
Pc.walca=2πr2+2πr*2R=2π*r(r+2R)
Pps=πR2
W ΔBFE:




 Tu masz wyjaśnione jak rysować taki przekrój.
http://www.zadania.info/d454/7037217
|MN|=a√2
Powstał sześciokąt foremny
Tu masz wyjaśnione jak rysować taki przekrój.
http://www.zadania.info/d454/7037217
|MN|=a√2
Powstał sześciokąt foremny


