ciągłość funkcji Madzia: a) ⎧ x² dla x>1 f(x)= ⎩ log₂x dla x∊(0,1) d) ⎧ e^−x dla x≤0 f(x)= ⎩ x dla x>0 narysuj wykres funkcji i zbadaj jej ciągłość w punkcie x₀ proszę o rozpisane obliczenia żeby było widać co z czego i tak dalej bo to jakaś katastrofa jest . Z góry dziękuje z wszelką pomoc

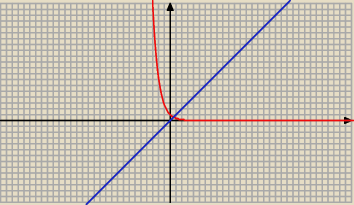
Janek191: d) f(0) = e⁰ = 1 oraz lim f(x ) = 0 x→ 0⁺ więc funkcja f nie jest ciągła w x₀ = 0 czyli nie jest ciągła w ℛ

J: a) chyba nie dokońca dokładnie przepisałaś treść ( nie wiadomo co jes w punkcie x =1) jeśli jednak dobrze, to funkcja jest nieciągła w punkcie x = 1, bo nie posiada w tym punkcie wartości)

J: @Janek191 ... badamy ciągłość w punkcie, nie w całej dziedzinie..

Janek191: Racja f nie jest ciągła w x₀ = 0

Gray: Jeżeli funkcja z przykładu jest dobrze określona (tj. 0 nie należy do jej dziedziny) to jest funkcją ciągłą. Pytanie o ciągłość funkcji w punkcie, który nie należy do jej dziedziny jest bezsensowne (i szkodliwe). Nie wiem co takie zadania wnoszą. Wiem, że niczego nie uczą. Potem na pytanie czy tg jest ciągły człowiek nie wiem co odpowiedzieć, ... bo przecież są punkty, które nie należą do jego dziedziny... Zapomina o tym, że to nie ma wpływu na ciągłość funkcji.

Madzia: a) jest dokładnie tak jak mam podane zadanie w arkuszu od wykładowcy. Dziękuje bardzo za odpowiedź

J: w przykładzie a) funkcja nie ma wartości w x = 1 ( nie x = 0 ), ale nawet jesli wartość funkcji będzie określona, to i tak funkcja będzie nieciągła w punkcie x = 1 , bo będzie miała dwie różne granice

Madzia: Czyli po prostu muszę uważać bo na kolokwium mogą być przykłady wprowadzające w maliny. A jak coś wychodzi nie tak to po prostu nie do końca mój błąd tylko taki przykład i nie panikować że nie znalazłam ciągłości.