Uzasadnij że traveler: W trójkącie ABC na boku AB obrano punkt M (M ≠A,M ≠B). Punkty K i L są odpowiednio środkami boków AC i BC. Uzasadnij, że pole czworokąta KMLC jest równie sumie pól trójkątów AMK i MBL.

pigor: ... , otóż to samo, ale nie tak samo : pola P₁= P₃ i P₂= P₄ jako pola odpowiednich par trójkątów o równych podstawach i równych wysokościach (rys.dzięki η), więc P_KMLC= P₃+P₄= P₁+P₂= P_ΔAMK+P_ΔBML c.n.uzasadnić . ....

pigor: ... , cóż mam inne zdanie, bo ja widzę u Ciebie tym razem przerost formy nad oczywistą treścią zawartą w treści zadania i tak naprawdę to do mojego uzasadnienia moglem wcale nie powoływać się na Twój ..."przesadzony" (za dużo informacji) rysunek ,no i to tyle. .

Eta: Narysuj choć jeden rysunek ( bo nigdy nie widziałam) zawsze liczysz "na sucho"

Eta: Zadowolony?

pigor: ..., masz rację, bo ... nie umiem i nie chcę umieć; zadowolona

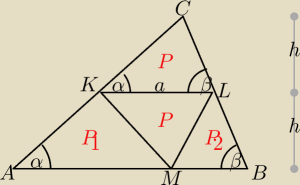
Bogdan: Trójkąty KLC i ABC są podobne w skali 1:2. Pole trójkąta KLC jest równe 1/4 pola trójkąta ABC. Pola trójkątów KLC i KLM są równe sobie, suma pól tych trójkątów jest równa 1/2 pola ABC, wobec tego suma pól trójkątów AMK i MBL też jest równa 1/2 pola trójkąta ABC. P + P = P₁ + P₂

PW: No to mi się przypomniała opowieść o jednym z profesorów. Asystenci twierdzili, że Profesor nigdy nie rysował w czasie wykładów, i swoim asystentom zalecał, żeby nie posługiwali się rysunkami. Przygotowując się do wykładu Pan Profesor zamykał się na godzinę w swoim gabinecie i nie wolno mu było przeszkadzać. Plotka głosiła, że wtedy ... robił sobie rysunki.