Pilne Ola : Dany jest trójkąt ABC o wierzchołkach: A(−7,−1), B(−1,−3), C(−5,1). a) Sprawdź, czy jest prostokątny. b) Oblicz jego pole. c) Wyznacz równanie okręgu opisanego na tym trójkącie.

marektg: rozwiązuje

marektg: rozwiązuje

Ola : ok

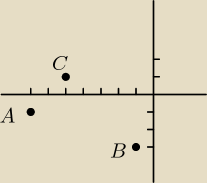
marektg: Z rysunku widać, że aby sprawdzić czy ten trójkąt prostokątny to AC2 + BC2 = AB2 AC = √(−7+5)2 + (−1−1)2 AC = √4+4 AC = 2√2 BC = √(−1+5)2 + (−3−1)2 BC = √16 + 16 BC = 4√2 AB = √(−7+1)2 + (−1+3)2 AB = √36 + 4 AB = 2√10 AC2 + BC2 = AB2 8 + 32 = 40 40 = 40 Trójkąt ABC jest prostokątny Pole trójkąta to: P = 12 * AC * BC P = 12 * 2√2 * 4√2 P = 8 Promień okręgu opisanego na trójkącie prostokątnym ma długość równą połowie przeciwprostokątnej, czyli R = AB2 R = √10 Środek przeciwprostokątnej jest środkiem tego okręgu S = ( xA + xB2 , yA + yB2 ) S = (−4 , −2) Równanie okręgu opisanego ( x + 4 )2 + ( y + 2 )2 = 10