 Byłabym bardzo wdzięczna, gdyby ktoś rozwiązał te zadania albo przynajmniej dał jakieś
podpowiedzi
Byłabym bardzo wdzięczna, gdyby ktoś rozwiązał te zadania albo przynajmniej dał jakieś
podpowiedzi  Błagam, zlitujcie się nad biedną maturzystą przed którą jeszcze 3 dni matur
...
Błagam, zlitujcie się nad biedną maturzystą przed którą jeszcze 3 dni matur
... Wrzucam skan, bo do jednego zadania potrzebny jest rysunek
Wrzucam skan, bo do jednego zadania potrzebny jest rysunek  http://i61.tinypic.com/2zt9cw4.jpg
http://i61.tinypic.com/2zt9cw4.jpg
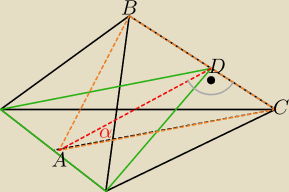 Zielony rysunek to dana plaszczyzna.
pomaranczowy trojkat jest równoramienny ( AB = AC = h ), wiec AD to jego wysokosc (bo BD = CD =
1/2BC)
Zielony rysunek to dana plaszczyzna.
pomaranczowy trojkat jest równoramienny ( AB = AC = h ), wiec AD to jego wysokosc (bo BD = CD =
1/2BC)
| |||||||||||
sin α = DC / AC = | |||||||||||
|
 zad. 7)
x − dlugosc trojkata rownobcznego z zadania. (a −podstawa, b −k. boczna)
x = a√2 (przekatna podstawy) i dl. x jest dl. srodkowej tr. o bokach a,b,b na bok b.
a√2 = U{√2a2 + 2b2 − b2{2} − wzor na srokowa (wyprowadzisz z tw. cosinusow )
zad. 7)
x − dlugosc trojkata rownobcznego z zadania. (a −podstawa, b −k. boczna)
x = a√2 (przekatna podstawy) i dl. x jest dl. srodkowej tr. o bokach a,b,b na bok b.
a√2 = U{√2a2 + 2b2 − b2{2} − wzor na srokowa (wyprowadzisz z tw. cosinusow )
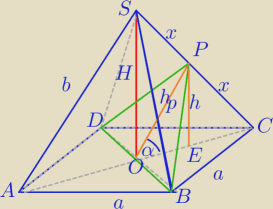 |DB|=a√2
|BP|=|DP| =a√2 z zał.
|DB|=a√2
|BP|=|DP| =a√2 z zał.
| a√6 | ||
hp= | − wysokość przekroju DBP | |
| 2 |
| 1 | ||
|OE|= | |OC| | |
| 2 |
| OE | √3 | |||
cosα= | = | |||
| hp | 6 |
| 6a2 | 2a2 | a√6 | a√2 | √3 | ||||||
x2= | + | −2* | * | * | ⇔ | |||||
| 4 | 4 | 2 | 2 | 6 |
| 3a2 | ||
x2= | ||
| 2 |
| a√3 | ||
x= | ||
| √2 |
| b |
| 2√3 | ||||||||||||
= | = | |||||||||||||
| a | a | √2 |
| a√768s2−a4 | ||
Mila, zadanie 2 teraz mi dobrze wyszło |  Dzięki , zaraz przeanalizuję 7 Dzięki , zaraz przeanalizuję 7 | |
| 24 |




