WYKRES FUNKCJI
155178: f(x)=2|sinx|cosx
Jak narysować taką funkcję ?
Oraz jak wyznaczyć zbiór wartośći :
f(x)=sinx−cosx
Zrobiłem to tak :
f(x)=sinx−cosx=√2(sinx√22−cosx√22)=√2(cosπ4sinx −
sinπ4cosx)=√2sin(x−π4)
Co zrobiłem nie tak oraz jak narysować wykres funkcji :
f(x)=sinx−cosx
24 lis 20:29
Saizou :
f(x)=2lsinxlcosx
dla sinx≥0 f(x)=2sinxcosx=sin(2x)
dla sinx<0 f(x)=2(−sinx)cosx=−sin(2x)
| | √2 | | √2 | | π | |
d(x)=sinx−cosx=√2( |
| sinx− |
| cosx)=√2sin(x− |
| ) |
| | 2 | | 2 | | 4 | |
24 lis 20:33
kyrtap: f(x) = 2IsinxIcosx
| | ⎧ | 2sinxcosx gdy sinx>0 | |
| f(x) = | ⎨ | |
|
| | ⎩ | −2sinxcosx gdy sinx<0 | |
| | ⎧ | sin2x gdy sinx>0 | |
| f(x) = | ⎨ | |
|
| | ⎩ | −sin2x gdy sinx<0 | |
24 lis 20:35
155178: Skąd to się wzięło ? Rozumiem rozpisanie dla sinx≥0 f(x)=2sinxcosx ale skąd tu się bierze
sin(2x) ?

OOO I jak narysowaćnp. 2sinxcosx ?
24 lis 20:42
155178: @ODŚWIEŻ
24 lis 21:31
Mila:
z wzoru sin(2x) =2sinx*cosx
24 lis 21:51
155178: Dobra to już ogarnąłem, ale jak narysować coś takiego
⎧ sin2x gdy sinx≥>0
f(x) = ⎨
⎩ −sin2x gdy sinx<0
24 lis 21:53
kyrtap: rysujesz sobie podstawową funkcję sinx i patrzysz względem niej jak rysować
24 lis 21:54
155178: Jak to ? No ja tak robiłem ale wychodzi mi inaczej niż w odpowiedzi ;\ Tam gdzie normalnie
sinus jest dodatni czyli od <0;π> rysowałem sin2x i wychodzi mi "garb" u góry i garb u dołu, a
powinny wyjść 2 u góry. Mógłbyś t narysować ?
24 lis 22:02
155178: @ODŚWIEŻ
24 lis 22:21
razor:
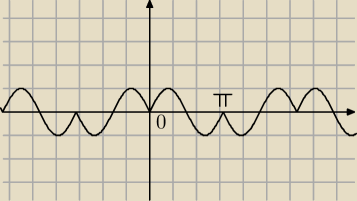
24 lis 22:25
155178: Mógłbyś to wytłumaczyć?

Jakoś krok po kroku ? Bo ja robiłem to także tam gdzie sinx jest
dodatni czyli <0;π>, <2π;3π> rysowalem sinx czyli po prostu zaczynałem w 0 i do
π2 garb
do góry a od
π2 do π garb w dół i właśnie nie wiem skąd się bierze taki rysunek jaki Ty
masz : P
24 lis 22:31
155178: @ODŚWIEŻ
24 lis 22:48
razor: tam gdzie sinx jest dodatni rysujesz sin2x
24 lis 22:51
155178:
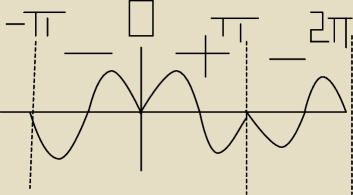
Wyjdzie coś takiego :
Tam gdzie − to znaczy że rysuję −sin2x, a tam gdzie + to rysuję sin2x ? A −sin2x to po prostu
odwrócony sinus ?

24 lis 23:03
155178: @ODSWIEZ
24 lis 23:44
 OOO I jak narysowaćnp. 2sinxcosx ?
OOO I jak narysowaćnp. 2sinxcosx ?

 Jakoś krok po kroku ? Bo ja robiłem to także tam gdzie sinx jest
dodatni czyli <0;π>, <2π;3π> rysowalem sinx czyli po prostu zaczynałem w 0 i do π2 garb
do góry a od π2 do π garb w dół i właśnie nie wiem skąd się bierze taki rysunek jaki Ty
masz : P
Jakoś krok po kroku ? Bo ja robiłem to także tam gdzie sinx jest
dodatni czyli <0;π>, <2π;3π> rysowalem sinx czyli po prostu zaczynałem w 0 i do π2 garb
do góry a od π2 do π garb w dół i właśnie nie wiem skąd się bierze taki rysunek jaki Ty
masz : P
 Wyjdzie coś takiego :
Tam gdzie − to znaczy że rysuję −sin2x, a tam gdzie + to rysuję sin2x ? A −sin2x to po prostu
odwrócony sinus ?
Wyjdzie coś takiego :
Tam gdzie − to znaczy że rysuję −sin2x, a tam gdzie + to rysuję sin2x ? A −sin2x to po prostu
odwrócony sinus ? 