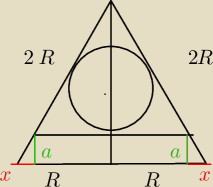
Pochodne i rachunek cz.2 Splifsta: 4. W stożek o promieniu podstawy R i tworzącej 2R wpisano walec i kule w sposób jak na rysunku. Kiedy suma objętości V walca i kuli będzie ekstremalna. Do czego doszedłem: Łatwo było zauważyc, że to trójkąt równoboczny czyli

	a
x =
	√3

	a
zatem r walca = R − x = R −
	√3

	a
Vwalca= π *( R −		)2 * a
	√3

Została kula. Dlatego ze to trójkąt równoboczny to możemy zająć się okręgiem wpisanym w trójkat równoboczny o boku 2R − 2x

	√3		a
jego wysokość h=		* (2R − 2x) = √3R − √3 *		= √3R − a
	2		√3

	√3R − a
Z tego że promień okregu wpisanego w taki trójkąt to 1/3 * h mam r kuli =
	3

	4		√3R − a
czyli mam już ostatnią rzecz V kuli =		* π * (		)3
	3		3

czyli nasza funkcja sumy objętości ma postać

	a		4		√3R − a
Vc= π *( R −		)2 * a +		* π * (		)3
	√3		3		3

Teraz trzeba przyrównać pochodna do zera żeby mieć ekstremum. Tylko, że ta pochodna wychodzi kosmiczna ;s i nie bardzo chce się przyrównywać do zera. Prosiłbym o pomoc. Nie wiem czy gdzieś mam błąd w rozumowaniu czy po prostu będzie dużo zabawy.

Adrian : Uzależnienic trzeba wysokość walca od jego promienia. promień walca to r, więc wysokość Walca to (R−r) √3 Podstawa nowego trójkąta równobocznego to 2r, zatem wysokość To r √3 Objętość kuli łatwo policzyć Dodając wszystko do siebie otrzymamy V= π √3 (Rr²−23r³/27) Miejsce zerowe pochodnej dla r=18/23 R