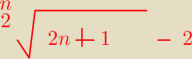24 lis 17:17
J:
| | sinx | |
= lim |
| *sinx = 1* 0 = 0 .. |
| | x | |
24 lis 17:21
Lukas:
Dzięki
a takie coś
n→
∞
| 2n+1+3n+1 | | 2n*2+3n*3 | |
| = |
| |
| 2n+3n | | 2n+3n | |
24 lis 17:27
J:
..mianownik: 3n(1 + (2/3)n) .. i granica = 3
24 lis 17:34
Lukas:
Masz jeszcze chwile bo jutro mam z tego kart i nie wiem niektórych przykładów.
x→0
| arctg(3x−9) | | 3arctg(x−3) | |
| = |
| |
| x2−9 | | (x−3)(x+3) | |
| | arctg(x−3) | | 3 | |
= |
| * |
| =1 |
| | x−3 | | x+3 | |
24 lis 17:42
Lukas: ?
24 lis 18:20
razor: x→0?
24 lis 18:23
Mila:
Nie możesz wyłączyc 3 z argument arcusa!
24 lis 18:54
Lukas:
to jak to zrobić ?
24 lis 20:25
Mila:
Do czego dąży x ? Do zera? Zobacz dokładnie treść.
24 lis 20:26
Lukas:
x→3
24 lis 20:27
Lukas: up
24 lis 20:43
bezendu:
lim
x→0
| arctg(3x−9) | |
| *3*(x−3) | | (3x−9) | |
| |
| |
| (x−3)(x+3) | |
24 lis 20:59
Mila:
Korzystasz z granicy specjalnej.
======================
| | arctg(3x−9) | |
lim x→3 |
| = |
| | x2−9 | |
| | arctg(3x−9) | |
=lim x→3 |
| = |
| | (x−3)*(x+3) | |
| | 3*arctg(3x−9) | |
=lim x→3 |
| = |
| | (3x−9)*(x+3) | |
24 lis 21:08
bezendu:

24 lis 21:09
bezendu:
x→3 oczywiście
24 lis 21:10
Mila:
Ta brzydka minka to dla mnie?!
24 lis 21:11
bezendu:
Nie, ta brzydka minka obrazuję, że nic nie umiem do kolokwium i mi się wszystko myli

24 lis 21:19
Mila:
Posłuchaj dobrej muzyki.
24 lis 21:21
Lukas:
x→0
=i mam problem z mianownikiem
| | sinx | |
sin3x=sinx*sin2x= |
| *x*sin2x ? |
| | x | |
24 lis 21:22
kyrtap: ale bezendu pieprzysz nie od rzeczy

24 lis 21:24
bezendu:
Muszę jeszcze coś porobić Mila masz jakieś zadania z funkcji odwrotnych i cyklometrycznych
?
24 lis 21:25
Mila:
| | sinx−sinx*cosx | |
= |
| = |
| | cosx*sin3x | |
| | 1−cosx | | 1−cosx | |
= |
| = |
| = |
| | cosx*(1−cos2x) | | (1−cosx)*(1+cosx)*cosx | |
| | 1 | | 1 | |
limx→0 |
| = |
| |
| | (1+cosx)*cosx | | 2 | |
24 lis 21:32
kyrtap: Mila naprawdę dobrze radzi abyś posłuchał muzyki

24 lis 21:33
Lukas:
pierwiastek (n/2) z 2n+1 i poza pierwiastkiem −2
24 lis 21:38
Lukas:
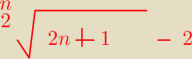
24 lis 21:39
Lukas:
n→∞
24 lis 21:49
Lukas: ?
24 lis 22:10
Mila:
(2n+1)2n=n√(2n+1)2→1
limn→∞[n√(2n+1)2−n)=−∞
24 lis 22:20
Lukas:
| | 2 | |
ale tam jest {n}{2} a nie |
| |
| | n | |
24 lis 22:24
Mila:
3√10=1013
n√10=101n
24 lis 22:26
Lukas:
ok, to jeszcze Panią pomęczę ! Mogę ?
24 lis 22:35
24 lis 22:57
razor: jest taki wzór
| | ln(1+an) | |
lim |
| = 1 przy an → 0 |
| | an | |
24 lis 22:59
24 lis 23:07
razor: | √x | |
| = x1/2−1/3 = x1/6 = 6√x → 0 |
| 3√x | |
24 lis 23:15
Lukas:
Dzięki razor.
24 lis 23:17
Mila:
Jutro, Łukasz, rozwiązywałam długi przykład Patrykowi.
Teraz dobranoc. Wrzuć problemy, jak wejdę jutro na forum, to popatrzę.
24 lis 23:51
Lukas:
Ok, może przełożymy tą kart. Dziękuję i dobranoc.
24 lis 23:56
Lukas:
Jest tu jeszcze ktoś?
25 lis 15:51
Lukas:
Wyjąsni mi ktoś funkcje odwrotne i cyklometryczne ?
25 lis 15:59
kyrtap: a co chcesz wiedzieć bo trochę nad tym siedziałem

25 lis 16:03
Lukas:
Wszystko co pomoże mi zaliczyć kart, wgl tego nie rozumiem.
25 lis 16:08
kyrtap: pokaż jakie masz zadania z cyklometrycznych powinienem umieć je zrobić
25 lis 16:09
Mila: ?
25 lis 16:10
Mila:
Wpisuj zadania, wyjaśnimy.
25 lis 16:10
Mila:
Pisz w nowym wątku.
25 lis 16:12