Zbiory Granica: Zaznaczyć na płaszczyźnie kartezjańskiej AxB: A={x∊R: |x|≥4 ↔ |x|≥1} B={a∊R: ax²+4x+a > 0}

PW: A co to ma znaczyć A={x∊R: |x|≥4 ↔ |x|≥1} ?

Granica: "Moduł z X większe równe 4 WTEDY I TYLKO WTEDY gdy moduł z x większe równe 1"

Saizou : to jest bez sensu np. dla 2 mamy ze 2≥1 jest okej ale 2≥4 jest to fałsz

Granica: To podpowiem. Zbiór B należy rozwiązać za pomocą prawa logicznego: (p↔q)↔[(p⋀q)⋁(¬p⋀¬q) Ale chodzi mi bardziej o zaznaczenie tego na płaszczyźnie. W zbiorze A mamy "iksy" czyli bez problemu. A zbiór B mamy współczynnik "a". I tu właśnie nie jestem pewny co z tym zrobić na rysunku.

PW: Czyli A jest zbiorem pustym? Może idzie o to, że moduł x ma być zawarty między 1 a 4? Nie rozwiązuję zadań o niezrozumiałej treści.

PW: Nie dorabiaj "logiki" do prostego zadania, mylą Ci się przedmioty, czy co? Sprawdź polecenie, bo jest bzdurne.

Granica: Tu właśnie trzeba logikę dorobić. No chyba że profesor matematyki jest na tyle głupi, że nie wie, co robi. Nic bzdurnego w tym poleceniu nie widzę.

Granica: I nie widziałem informacji, że mamy tu wstawiać zadania na poziomie podstawowki/gimnazjum, więc wstawiam na poziomie wyższym. Jak ktoś czegoś nie wie, to raczej nie powinien zgrywać mądrali, bo to dobrze o nim nie świadczy.

PW: Rozumiem, profesor. Zamiast napisać zrozumiale definicję zbioru A, zadał zagadkę logiczną. Normalni ludzie tak nie robią. No, masz rację, źle to o mnie świadczy. Poddaję się, myślałem że polecenie jest źle przepisane, co jest tu rzeczą nagminną − ludzie się skręcają, wymyślają cuda, a pytający na końcu pisze: sorry, powinno być inaczej. Ale widzę, że potrafisz to rozwiązać − o 15:29 wyjaśniłeś, więc po co pytasz?

Granica: Mysle, że to nie kwestia, że to profesor, tylko kwestia, że to studia. Po prostu trzeba raczej sobie utrudniać przykłady, a nie ułatwiać. Ale chodzi mi o zaznaczenie tego na rysunku, na płaszczyźnie. Przypuśćmy, że zbiory wyszły tak: A: x∊(−∞,−4> ∪ (−1,1) ∪ <4,+∞) B: a∊(2,+∞) Nie pamiętam, jak mi powychodziło, jak liczyłem, więc przypuśćmy, że to co napisałem wyżej jest dobrze. Jak zaznaczyć to na płaszczyźnie?

Saizou : B liczysz ze względu na x a nie przez a

Granica: To czemu zbiór ten jest okreslony współczynnikiem a? Trzeba zagwarntowac, że Δ<0 i że a>0 wychodzi to, co napisałem wyżej. Co dalej?

PW: To mają być pary (x, a), w których x∊A i jednocześnie a∊B, czyli na rysunku będzie to suma trzech podzbiorów płaszczyzny: − "nieskończony prostokąt" o podstawie x∊(−∞, −4> i drugim boku y∊(2, +∞) − "nieskończony prostokąt" o podstawie (−1 1) i drugim boku jak wyżej − "nieskończony prostokąt" symetryczny do tego pierwszego względem osi OY. Niefachowe określenia, ale na rysunku ich nie będzie widać. Trzeba by chyba dodać kolory i legendę, który kolor oznacza, że punkty należą do zbioru, a który − że nie należą (myślę o półprostych "brzegowych" opisanych równościami x = −4 i y > −2, x = −1 i y > 2, x = 1 i y > 2, x = 4 i y >2 x ≤ −4 i y = 2 i tak dalej).

PW: Saizou, myślę, że jednak ze względu na a. O iksach występujących w tej definicji nie mówi się nic, a jest taka niepisana umowa, że jak nie mówi się nic − to znaczy że dla wszystkich. Na tej zasadzie mówi się, że x = 5 jest prostą na płaszczyźnie (o igrekach nie mówi się nic, to znaczy że mogą być jakiekolwiek).

Granica: Ktoś się podejmie rysunku?

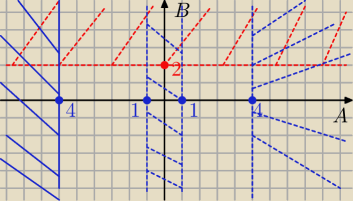
Gray: Twoje to co na czerwono i niebiesko jednocześnie.

Granica: DZIĘKI WIELKIE