Matura
McArtur Artur: Dany jest trojkat ABC, gdzie A=(−3,−2), B=(1,−1), C=(−1,4). Wyznacz rownanie symetralnej boku
AC tego trojkata.
No i udalo mi sie ustalic ile wynosi a i b. a=3, b=7. Ale nie mam pojecia co dalej.
23 lis 17:57
Mila:
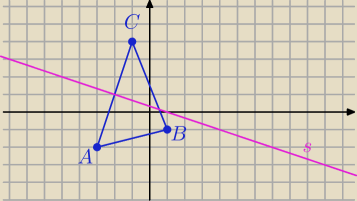
Symetralna odcinka to zbiór wzystkich punktów jednakowo odległych od końców odcinka.
P(x,y) punkt symetralnej odcinka AC.
|AP|=|PC|
√(x+3)2+(y+2)2=
√(−1−x)2+(4−y)2 /
2⇔
(x+3)
2+(y+2)
2=(−1−x)
2+(4−y)
2⇔wykonaj obliczenia:
.
..
| | 1 | | 1 | |
s: y=− |
| x+ |
| równanie symetralnej AC |
| | 3 | | 3 | |
23 lis 18:07
Eta:
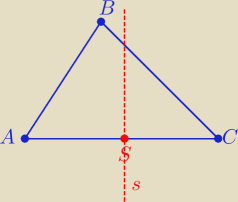
Inny sposób:
Symetralna boku AC , to prosta prostopadła do prostej AC i przechodzi
przez środek odcinka AC
| | 4+2 | | 1 | | xA+xC | | yA+yC | |
aAC= |
| =3 to as= − |
| i S( |
| , |
| )=(−2,1) |
| | −1+3 | | 3 | | 2 | | 2 | |
| | 1 | | 1 | | 1 | |
s: y= − |
| (x−xS)+yS ⇒ s : y= − |
| x+ |
| |
| | 3 | | 3 | | 3 | |
23 lis 18:23
McArtur Artur: Wspolrzedne punktu P odczytujemy z rysunku?
A jak beda nieczytelne? Mozna je jakos obliczyc?
23 lis 18:26
McArtur Artur: Pytanie o wspolrzedne do sposobu Mili.
23 lis 18:29
Mila:
Jeżeli masz podane wsp. końców odcinka to piszesz równanie i już .
Punkt P=(x,y) jest ogólnie przyjęty, potrzebne wsp. końców odcinka.
23 lis 21:54