pochodne Efka: Wyznacz wartości ekstremalne funkcji, badając ich przebieg: a) f(x)=−x³+3x+2 dla x∊[0,2] b) f(x)=2x⁷ − x⁵ dla x∊[0,3]

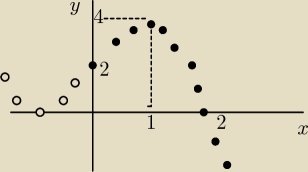
AS: a) f(x) = −x³ + 3*x + 2 dla x ∊ [0,2] Obliczam pochodną f(x) f'(x) = −3*x² + 3 = −3(x² − 1) Wyznaczam ekstrema f'(x) = 0 ⇔ x = −1 lub x = 1 Wartość −1 odpada bo wykracza poza przedział badania [0,2] Dla x ∊ (0,1) f'(x) > 0 funkcja rośnie dla x ∊ (1,2) f'(x) < 0 funkcja maleje dla x = 1 funkcja osiąga maksimum,które wynosi 4 Badam wartości krańcowe funkcji f(0) = −0³ + 3*0 + 2 = 2 f(2) = −2³ + 3*2 + 2 = 0 W przedziale [0,2] funkcja osiąga maksimum (1,4) i jest to wartość zarazem największa w badanym przedziale, wartość najmniejszą osiąga dla x = 2 równą 0.

Efka: dziękuję za pomoc! do przykładu b) pochodna wynosi 14x⁶−5x⁴ ? jeśli tak to ekstrema wychodzą 0 i w przybliżeniu 0,6 i −0,6 ? czy coś źle policzyłam?

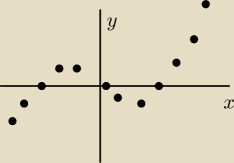
AS: b) f(x) = 2*x⁷ − x⁵ w [0,3] Miejsca zerowe f(x) = 0 ⇔ x = 0 lub x = ± 1/√2 ≈ 0.7071 Pochodna funkcji f'(x) = 14*x⁶ − 5*x⁴ = x⁴*(14*x² − 5) f'(x) = 0 ⇔ x = 0 lub x = ± √5/14 ≈ ± 0.5976 resztę proszę samemu dokończyć

AS: Pamiętaj o przedziale [0,3] − tylko ten obszar nas interesuje.