parametry funkcji kwadratowej ania: Dla jakich wartości parametru m nierówność (x−3m)(x−m−3)<0 jest spełniona przez każdą liczbę rzeczywistą należącą do przedziału <1;3>

ania: Proszę o wytłumaczenie po kolei ,a nie tylko samo rozwiązanie

ania: pomoze ktos?

J: f(x) = (x−3m)(x−m−3) = .... Warunki: 1) f(1) < 0 2) f(3) < 0

Eta: jeszcze 3) 1<x_w<3

ania: na wierzcholek nie potrzeba,prędzej na deltę

J: dlaczego..? skoro a = 1....

J: Δ nie ma tu nic do rzeczy...

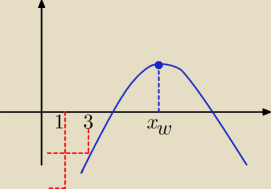
Eta: i co ? potrzeba? czy nie?

Eta: O kurcze .... zobaczyłam − x²

J: a = 1 ...

ania: oczywiście,że ma .. przecież musimy założyć ,że istnieją te dwa miejsca zerowe i do tego potrzebna nam delta

ania: prawda?

Ditka: może tak: x₁,x₂∊(−∞,1)∪(3,+∞) z postaci f(x): x₁=3m x₂=m+3 musi więc być 3m<1 ∧ m+3>3 ⋁ 3m>3⋀m+3<1 m<¹₃⋀m>0 ⋁ m>1 ⋀ m<−2 m∊(0,¹₃) ⋁ m∊Φ odp. m∊(0,¹₃)

Ditka: poprawka, źle zapisałam powinno być x₁∊(−∞,1) x₂∊(3,+∞) albo odwrotnie , chodzi o to że nie mogą być oba w jednym z przedziałów , muszą "obejmować" przedział <1,3>