zespolone
Kaktus:
Jak to narysować i rozwiązać
Jak to narysować ?
22 lis 15:33
Kaktus: ?
22 lis 15:51
Kaktus: ?
22 lis 16:46
Gray: | | x | |
Im(ix−y) = x, czyli |
| >x . |
| | x2+y2 | |
To chyba zmienia wszystko...
22 lis 17:00
ICSP: Nie podoba mi się druga linijka, tak jakby czegoś tam brakowało

22 lis 17:01
Kaktus:
Czego brakuję ?

22 lis 17:07
Gray: Ja się tego nie doczepiłem, ale faktycznie − brakuje )
22 lis 17:08
Gray: Jest może nawet zbyt dużo (o Re), ale formalnie błędem to nie jest.
22 lis 17:09
Kaktus:
Z definicji mam takie coś
| 1 | | x | | −y | |
| =( |
| , |
| ) |
| z | | x2+y2 | | x2+y2 | |
22 lis 17:10
Gray: Rozwiązałeś tę nierówność z 17:00?
22 lis 17:47
Kaktus: nie
22 lis 18:10
Gray:
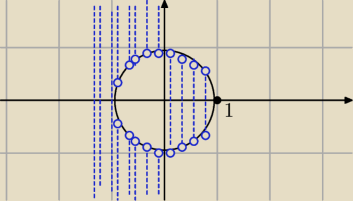
Dlaczego?
| x | |
| >x ⇔ a) x> 0 i 1>x2+y2 albo b) x<0 i 1<x2+y2 |
| x2+y2 | |
x
2+y
2 = 1 to równanie okręgu o środku w (0,0) i promieniu r=1. Twój obszar to to zakreskowane
(bez okręgu).
22 lis 18:17
Dziadek Mróz:
| | 1 | | 1 | | x − iy | | x − iy | | x | |
Re( |
| ) = Re( |
| * |
| ) = Re( |
| ) = |
| |
| | z | | x + iy | | x − iy | | x2 − y2 | | x2 − y2 | |
Im(iz) = Im(i(x + iy)) = Im(ix − y) = x
22 lis 18:23
Gray: Od kiedy (x+iy)(x−iy) = x2 − y2 ?
22 lis 18:24
Kaktus:
Dziękuję
22 lis 18:38
Kaktus:
a jak na płaszczyżnie zespolonej narysować to
|z−3i|>|z|
|z−3i|>|x
2+y
2|
22 lis 18:44
Gray:
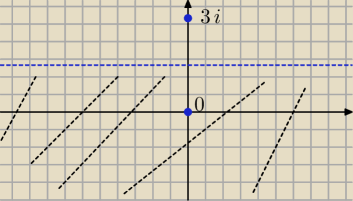
Nie rozpisuj tego:
|z−3i|>|z−0| → to jest zbiór liczb zespolonych, których odległość od liczby 3i jest większa niż
od 0. Jest to więc dolna półpłaszczyzna, której brzegiem w układzie Oxy jest prosta y=3/2 (to
zakreskowane na czarno).
22 lis 20:07
Kaktus:
Właśnie ale |z−3i|> więc chyba obszar nad symetralną a nie pod nią ?
22 lis 20:13
Mila:
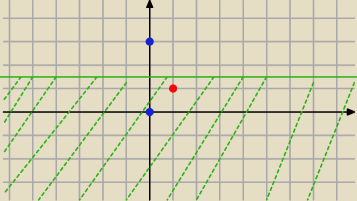
Niech z=(1,1)⇔z=1+i∊obszaru poniżej symetralnej
Sprawdzam:
|1+i−3i|=|1−2i|=
√12+22=5
|z|=p{1
2+1
2|=
√2⇔
|1+i−3i|>|1+i|
Zgodnie z zapisaem
Gray'a
22 lis 20:25
Kaktus:
ale czemu poniżej skoro 3i>0
22 lis 20:37
Kaktus: ?
22 lis 21:01
Mila:
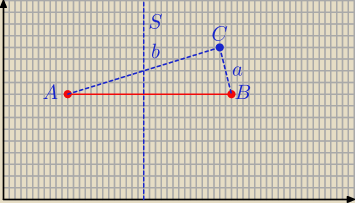
Na symetralnej leżą punkty równo odległe od A i B.
Odległość punktu C od punktu A jest większa niż jego odległość od punktu B.
b>a
Twoje zadanie patrz 20:25
Połącz czerwony punkt C z punktem A(0,3) i B(0,0)
|AC|>|BC|
22 lis 21:11
Kaktus:
Ok, właśnie nie mogę zrozumieć tych warunków, pomożesz Bogini ?

22 lis 22:11
Mila:
Przecież to geometria na płaszczyźnie, przeczytaj uważnie. Symetralna już w gimnazjum była.
Czytaj tekst 21:11.
Narysuj na kartce odcinek, jego symetralną i mierz linijką odległości dowolnego punktu
(nie leżącego na symetralnej )od końców odcinka.
Z lewej strony s punkty są bliżej A niż B.
Z prawej strony s punkty są dalej od A ale bliżej B.
22 lis 22:18
Kaktus:
Ale nie chodzi mi teraz o symetralną, tylko inne jeszcze przykłady. W środę mam kolkowium i
chciałbym sie tego nauczyć.
22 lis 22:19
Mila:
Pisz o co chodzi.
22 lis 22:33
Kaktus:
czyli mając
|z+3i|<|z−1−4i|
|z−(−3i)|<|z−(1+4i)|
Dobrze ?
22 lis 22:42
bezendu: ?
22 lis 23:01
Mila:
Nie.
Mają być punkty bliżej (0,−3i) niż (1,4)
Jeśli nie wiesz jak zaznaczyć obszar, to wybierz jeden punkt ("łatwy") i sprawdź nierówność.
Jeśli będzie prawdziwa , to obszar z tym punktem , jesli nie to drugi obszar.
P=(0,0)
|0+3i|=3
|0−1−4i|=[
√1+16=√17
3<√17
Obszar pod symetralną.
22 lis 23:03
Kaktus :
|z2+2iz−1|<9
|z(z+2i)−1|<9
22 lis 23:05
Mila:
z2+2iz−1=(z+i)2
( mogłeś obliczyć Δ i dojść do tego)
Teraz rozwiązuj
22 lis 23:19
Kaktus : Teraz to będzie
|(z+i)|<9
okrąg o środku −1 i promieniu 9
22 lis 23:26
Mila:
|(z+i)2|<9
|(z+i)*(z+i)|<9
|z+i|2<9
|z+i|<3
wnętrze okręgu o środku S=(0,−1) i r=3
23 lis 00:14
Kaktus :
dziękuję.
23 lis 00:16


 Dlaczego?
Dlaczego?
 Nie rozpisuj tego:
|z−3i|>|z−0| → to jest zbiór liczb zespolonych, których odległość od liczby 3i jest większa niż
od 0. Jest to więc dolna półpłaszczyzna, której brzegiem w układzie Oxy jest prosta y=3/2 (to
zakreskowane na czarno).
Nie rozpisuj tego:
|z−3i|>|z−0| → to jest zbiór liczb zespolonych, których odległość od liczby 3i jest większa niż
od 0. Jest to więc dolna półpłaszczyzna, której brzegiem w układzie Oxy jest prosta y=3/2 (to
zakreskowane na czarno).
 Niech z=(1,1)⇔z=1+i∊obszaru poniżej symetralnej
Sprawdzam:
|1+i−3i|=|1−2i|=√12+22=5
|z|=p{12+12|=√2⇔
|1+i−3i|>|1+i|
Zgodnie z zapisaem Gray'a
Niech z=(1,1)⇔z=1+i∊obszaru poniżej symetralnej
Sprawdzam:
|1+i−3i|=|1−2i|=√12+22=5
|z|=p{12+12|=√2⇔
|1+i−3i|>|1+i|
Zgodnie z zapisaem Gray'a
 Na symetralnej leżą punkty równo odległe od A i B.
Odległość punktu C od punktu A jest większa niż jego odległość od punktu B.
b>a
Twoje zadanie patrz 20:25
Połącz czerwony punkt C z punktem A(0,3) i B(0,0)
|AC|>|BC|
Na symetralnej leżą punkty równo odległe od A i B.
Odległość punktu C od punktu A jest większa niż jego odległość od punktu B.
b>a
Twoje zadanie patrz 20:25
Połącz czerwony punkt C z punktem A(0,3) i B(0,0)
|AC|>|BC|

 czyli mając
|z+3i|<|z−1−4i|
|z−(−3i)|<|z−(1+4i)|
Dobrze ?
czyli mając
|z+3i|<|z−1−4i|
|z−(−3i)|<|z−(1+4i)|
Dobrze ?