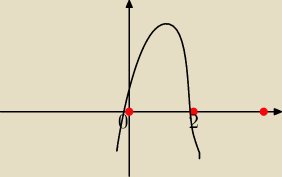
jh kinder: Wyznacz ekstrema funkcji f(x)= 4x / x²+1 df=r/{3} Wyszło mi tyle f'(x) = −2x³ + 10x² − 12x / (2x−6)² potem wychodzi x(−2x² + 10x −12)=0 x=0 x1=3 x2=2 f(0)=0(minimum) dobry wynik? f(2)= 0(maksimum) ? tutaj tez nie jestem pewnien

===: ... jakieś herezje wypisujesz ...

kinder: czemu?

kinder: sorrki to powinno byc f(x)= x² / 2x−6

===: jaka jest dziedzina?

===: no tak ....zgaduj−zgadula ...

kinder: wszystkie liczy rzeczywiste z wyłaczeniem 3 taka jes dziedzina

===: skoro nie potrafisz wpisać treści ....to już nie mam chęci na zabawę −

kinder: jakiej tresci?

kinder: e pomoze ktos

===: ...już pochodna źle

kinder: a no faktycznie sorrki za moze głupie błedy pochodna to 2x²−12x wtedy x =0 x=6

===: dokładnie

kinder: polegne na maturze przez mój pospiech

===: ... to nie pośpiech ... to "bylejakośc" −

kinder: f(0)= 0 maksimum f(6)=0 minimum

kinder: moze byc i to

kinder: a jak mamy wyznaczyc dziedzine w tym przypadku to 2x−6≠0 x≠3 to te 3 oznaczamy na wykresie?

===: dziedzinę możesz zapisać Ale jeśli rysujesz wykres funkcji ... to masz asymptotę

kinder: aha czyli dziedzina rozgranicza jedno monotonicznosc na dwie

kinder: ok dzieki

===: to nie całkiem tak −

kinder: tzn wiem o co chodzi ale nie umiem tego opisac