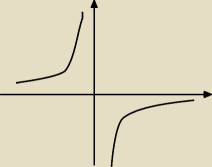
funkcja homograficzna Bartek: Posłuchajcie, czy może mi ktoś wyjaśnić dlaczego w krysickim nazwali tę funkcję funkcją rosnącą? Czy może być prawdą, że funkcją rosnąca znajduje się w drugiej i czwartej ćwiartce? Tzn. rozumiem,że I pochodna jest stale dodatnia, ale zawsze mi się wydawało, że gdy funkcja jest w II i IV ćw., to mówi się, że jest malejąca np. funkcja liniowa, czy nie tak? To jest wzór:

	2x−3
y=
	x+1

Wykres trochę przekłamałem, bo nie widać pionowej asymptoty.

Bartek: Chodziarz z drugiej strony...może po prostu głupi jestem i tyle.

Bogdan:

	2x − 3
y =
	x + 1

Tu można rysować wykresy funkcji

PW: Odpowiedź na postawione pytanie brzmi: funkcja jest rosnąca na przedziale (−∞, −1) i jest rosnąca na przedziale (−1, +∞). Rosnąca w całej dziedzinie oczywiście nie jest.

Bartek: PW, ja to akurat wiem, tylko przez chwilę strzeliło mi coś do tego pustego łba, że każda funkcja rosnąca musi koniecznie być w I i III ćw., a przecież to nie prawda, patrz. funkcja kwadratowa, prawda? No nie ważne. Tak czy siak dzięki