aa Hugo: czemu to jest zle log₃(2x−7) <=2− log₃(8−x) log₃(2x−7) <=log₃9 − log₃(8−x) OPUSZCZAM LOGI 2x−7 <= 9 −8+x x<=8

Dawid:

	x
Jak masz log39 − log3(8−x) wykorzystaj wzór loga
	y

PW: Nie ma takiego twierdzenia, które pozwalałoby "opuszczać logarytmy" − za takie coś mój profesor w liceum stawiał dwóję.

Hugo: ja tam na agh jutro kolos no dzieki

bezendu: Oj Hugo

Hugo: kurde −,− przenosze na prawą strone (2x−7)(8−x) −2 <= 0 wymnazam 16x −2x² −56 +7x −2 <=0 23x −2x² −58 <=0 Δ= 489 −,−?

Hugo: dobra nie wazne juz wiem o co chodzi xd

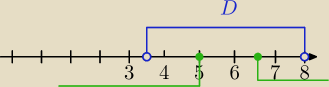
Mila: log₃(2x−7) <=2− log₃(8−x) D: 2x−7>0 i 8−x>0

	7
x>		i 8>x
	2

	7
x∊(		,8)
	2

log₃(2x−7)+log₃(8−x)≤2⇔ log₃[(2x−7)*(8−x)]≤log₃(9) teraz możesz porównać argumenty [(2x−7)*(8−x)]≤9 16x−2x²−56+7x−9≤0 −2x²+23x−65≤0 Δ=23²−4*2*65=529−520=9

	−23−3		26		−23+3
x=		=		=612 lub x=		=5
	−4		4		−4

x≤5 lub x≥6¹₂ i x∊D⇔

	7
x∊(		,5> ∪<612,8)
	2

====================