Różne miejsca zerowe funkcji z parametrem z dodatkowym warunkiem
DamianCH: Mam problem z drugim warunkiem, właściwie to chyba dobrze robię ale nie wiem jak zebrać
rozwiązanie na koniec wszystkich warunków : Dla jakich wartości parametru m
f(x)=x2−(m+1)+m2−1 ma dwa różne miejsca zerowe x1,x2 takie , że |x1|+|x2|>√5 . Z I
warunku delta>0 wychodzi mi przedział (−1,123) później ze wzoru Vieta suma x1,x2 to
−b/a czyli |m+1|>√5 i wychodzą II przedziały. Dobrze robię, czy trzeba jakiś dodatkowy
warunek ?
18 lis 20:22
wmboczek: raczej podnoś warunek do kwadratu − to co napisałeś zależy od znaków pierwiastków i zmienia się
w przedziale delty
18 lis 20:28
Tadeusz:
dla Ciebie |x
1|+|x
2|=x
1+x
2 
?
18 lis 20:28
DamianCH: Tadeusz przecież napisałem moduł z x1+x2 −b/a (z Viety) napisałem to dalej w module z Viety
wychodzi |m+1|
18 lis 20:31
DamianCH: wmboczek nie chciałem podnosić do kwadratu, gdyż w odpowiedziach jest z pierwiastkiem z 5
przedział
18 lis 20:32
Tadeusz:
czort swoje pop swoje
bierzesz −b/a i to przyrównujesz do √5 czyli zrównujesz x1+x2 z |x1|+|x2|
18 lis 20:40
DamianCH: nie można tak zrobić |x
1|+|x
2| na jeden moduł |x
1+x
2| ? Jeżeli cały czas to źle robię to
powiedz mi jak można ten warunek rozwiązać to spróbuję zrobić
18 lis 20:42
DamianCH: i wtedy jak mam moduł |x1+x2| to myślałem, że mogę tak samo zrobić moduł |−b/a|
18 lis 20:45
DamianCH: Czy może ktoś mnie nakierować co i jak, próbowałem też z kwadratami tego drugiego warunku jak
podpowiadał wmboczek ale też nie wyszło
18 lis 21:00
Eta:
x1≠x2
|x1|+|x2| >5 obydwie strony nieujemne to:
x12+x22+2|x1*x2|> 25
(x1+x2)2−2x1*x2+2|x1*x2|>25
teraz działaj ze wzorami Viete'a i rozpatrz 2 przypadki na moduł!
18 lis 21:10
DamianCH: Eta tylko , że suma modułów x1 x2 ma być >√5
18 lis 21:19
Eta:
Na jedno wychodzi
( źle spojrzałam)
To nie potrafisz poprawić? to samo, tylko po prawej (
√5)
2= 5 zamiast
25
18 lis 21:24
DamianCH: Wyszło mi coś takiego −m2+2m+3+2|m2−1|>5 i jak to dalej pociągnąć ? Na dwóch przedziałach
zależnych od wyrażenia w module czy po prostu moduł dodatni i ujemny ?
18 lis 21:24
Eta:
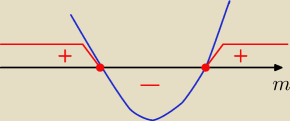
Rozpatrz dla 1
o m∊(−
∞, −1> U < 1,
∞) |m
2−1|= m
2−1
dla 1
o m∊(−1,1) |m
2−1|= −m
2+1
teraz dokończ .............
18 lis 21:29
DamianCH: No czyli przedział zależny od wyrażenie w module dzięki
Już robię zaraz zobaczymy co wyjdzie
18 lis 21:32
DamianCH: Kompletnie nic nie wyszło, tzn z drugiego warunku mam m należy do (1−
√5;1+
√5) ale w
połączeniu z pierwszym czyli m należy do (−1,4/3) dalej nie wychodzi odpowiedź z książki
możesz proszę zrobić całe zadanie ?
18 lis 21:46