Argument liczby zespolonej riv: Znaleźć argument liczby zespolonej z=(1+i√3)(1−i)

Gray: Argument iloczynu to suma argumentów (plus 2kπ):

	π		π
arg(1+i√3)(1−i)=arg(1+i√3) + arg(1−i) +2kπ=		−		+2kπ
	3		4

riv: ale ogólnie argument w zespolonych to liczby fi, więc skąd się to bierze

razor: arg(z*w) = argz + argw − do zapamiętania

	z
analogicznie arg(		) = argz − argw
	w

Gray: Bierze się to ze sposobu w jaki mnożymy liczby zespolone zapisane w postaci trygonometrycznej: moduły się mnoży, a argumenty właśnie dodaje.

riv: a wynik skąd sie bierze?

riv: czyli liczymy moduł z 1+i√3 i 1−i ?

riv: i potem fi? bo z pierwszego mi wychodzi II/3 a z drugiego 3II/4 i dalej nie wiem co dopisywać te 2kpi bo w wzorach z wykładu tego nie mam

Gray: Z drugiego może być np. −π/4. Możesz dodać do tego wielokrotność 2π i też będzie. Ale 3π/4 nie może być, bo cos(3π/4) = −√2/2 a sin (3π/4)= √2/2, więc to argument (−1+i) a nie (1−i). Dodaję wielokrotność 2π bo arg jest funkcją okresową o takim właśnie okresie.

riv: ok, ale to z czego bierze się to −pi/4 ? Liczy się to z czegoś?

riv: 1−i |z|=2

	√2
sin fi = −
	2

	√2
cos fi =
	2

czyli ćwiartka 2: π − π/4= 3π/4 nie wiem jak inaczej

Gray: W drugiej sin jest dodatni

riv: Fakt ale gafa oczywscie 4 ćwiartka. Ale to wtedy fi mi wyjdzie 7pi/8

riv: a w 1+i√3 wychodzi moduł = 2 ćwiartka pierwsza, czyli a₀=pi/6

riv: oczywiscie 1 cwiartka xd

Gray: Popatrz na to co Ci napisałem o 19:29 → udało mi się nie pomylić i wszystkie kąty są dobrze wyznaczone.

riv: Ok wyszło mi pi/3.. A z tego drugiego mi wychodzi dalej cwiartka 4 czyli fi = 2 pi − pi/4 = 7pi/4. Wiec skąd u Ciebie taki wynik. Doczekam bo chce to zrozumieć w końcu

riv: *dociekam

riv: Podbijam

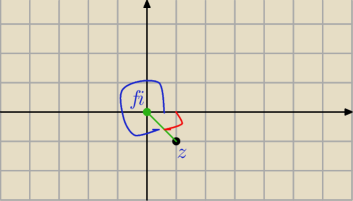
Mila: liczba (1−i) to na płaszczyźnie punkt (1,−1)

	π		7π
φ=2π−		=
	4		4

	π
Gray zapisał ten kąt jako ( −		) ( czerwony łuk) korzystając z tego, że
	4

	7π
wartości sinusa i cosinusa są takie same jak, dla kąta
	4

riv: Teraz już jaśniej ale jeśli napisalbym 7pi/4 to nie byłby błąd?

Mila:

	7π
Nie byłoby błędu. Argument		− dobrze.
	4

Gray: Nie, możesz tam wpisać 7π/4 plus dowolną całkowitą wielokrotność 2π. _______________________ Cześć Mila.

riv: Dziękuję za pomoc