pochodne ka: Jak pochodna jest 1) >1 to wartości rosną szybciej niż argumenty 2) 1 to rosną tak samo 3) >0 i <1 to rosną wolniej niż argumenty 4) 0 funkcja jest stałą 5) <0 wartości funkcji maleją dobrze rozumiem?

J : na razie prawdą jest: 4) i 5) .. reszta nie bardzo...

ka: to jaka jest prawda?

ka: ok, pochodna z np 3x to 3 czyli na jednego x, y wzrasta o 3. gdzie tu błąd?

ka: zzzz

b.: Uściślijmy: ,,Jak pochodna *na jakimś przedziale* jest...'' i wtedy jest wszystko OK.

ka: a jak nie ma tego "na jakimś przedziale" to czemu jest źle? Jak nam wyjdzie pochodna 2 to w jakiej sytuacji miałoby być inaczej niż napisałam?

Gray: Np. funkcja może mieć pochodną równą zero, a może nie być funkcją stałą; pochodna może być dodatnia a funkcja może nie być funkcją rosnącą, itp., itd.

ka: No to tego nie rozumiem, jak pochodna może być dodatnia skoro funkcja maleje?

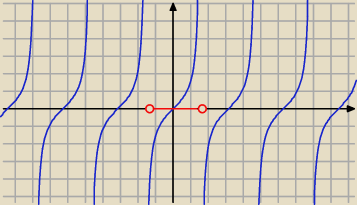
Gray: Nie napisałem, że funkcja maleje, tylko że nie jest rosnąca. Spójrz na wykres. To tangens. Jego

	1
pochodna to		; jest stale dodatnia, a tangens nie jest funkcją rosnącą. Psuje się,
	cos2x

gdyż nie jest funkcją określoną na przedziale. Ograniczając się do któregokolwiek przedziału, np. (−π/2,π/2) − na wykresie na czerwono, wszystko jest OK.

ka: Aha, rozumiem. Rzeczywiście, ale tangens jest specyficzny a w przypadku zwykłych funkcji, można spokojnie polegać na tych zasadach wyżej, tak?

Gray: Jeżeli są określona na przedziale (tj. dziedzina jest "jednokawałkowa", matematycy mówią spójna) to tak, jeżeli nie to nie.