ciągłość Cami: Potrzebuję pomocy czy może mi ktoś wytłumaczyć co to jest funkcja ciągła? ale nie definicjami cauchiego ani heinego, tak własnymi słowami?

J : Funkcja ciągła w punkcie: 1) posiada wartość w tym punkcie 2) posiada granicę w tym punkcie ( lewostronna = prawostronna) 3) granica jest równa wartości funkcji ..

Cami: hmmm.... nadal nie czaje.... a jakoś tak łatwiej?

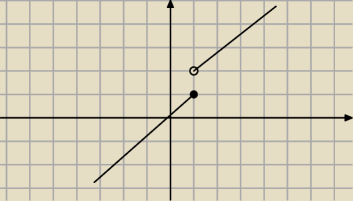
J : funkcja nie jest ciągła w punkcie : x = 1 ma wartość, ale nie ma granicy ..

Cami: bo mam przykłady z lekcji: f(x)=1/x ; x≠0 i tutaj dziedzina to R/0 wiec to 0 nie nalezy do dziedziny co mi daje ze nie mozna mowic o ciaglosci lub nieciaglosci w zb. ale za to f(x) {1/x ; x≠0 ciągła {1 ;x+0 nieciągła (napisalem funkcje klamerkowa) czemu?

razor: bo lim_x→0 nie istnieje (sprawdź granice jednostronne)

Cami: a czy mogę prosić jeszcze bez granic? bo nam wprowadzono ciaglosc a dopiero potem granice....

PW: Intuicyjnie ciągłość to możliwość narysowania wykresu bez odrywania ołówka od papieru. Komu taka intuicja nie daje zadowolenia, musi nauczyć się definicji, których tak nie chcesz..

Cami: czy w ogóle ktoś potrafi wytłumaczyć ciągłość funkcji bez granicy?

Cami: ok def Funkcja ciągła to taka, dla której mała zmiana argument daje małą zmianę wartości. Cauchiego: Niech f:A→R, A⊂R. Funkcję nazywamy ciągłą gdy dla każdego punktu zachodzi x₀∊A dla wszyst. epsilon>0 istn. delta>0 dla wszyst. x∊A zachodzi Ix−x₀I<delta ⇒If(x)−f(x₀)I<epsilon Heinego dla każdego ciągu x_n→x₀ zachodzi f(x_n)→f(x₀)

Cami: co dalej mi nie pomaga w ogarnięciu dlaczego raz dla funkcji 1/x jest ciągłość innym razem jej nie ma

Cami: help....

Cami: niech mi to ktoś wytłumaczy błagam

PW:

	1
Funkcja f(x) =		jest ciągła, co to za herezje?
	x

W tym momencie widać wyższość ścisłej definicji nad intuicją. Dziedzina tej funkcji składa się z dwóch przedziałów otwartych. Zero nie należy do dziedziny, więc pytanie o ciągłość w zerze jest niesensowne.

Cami: no właśnie tutaj się gubię.... f(x)=1/x ; x≠0 i tutaj dziedzina to R/0 wiec to 0 nie nalezy do dziedziny co mi daje ze nie mozna mowic o ciaglosci lub nieciaglosci w zb. ale za to f(x) {1/x ; x≠0 ciągła {1 ;x+0 nieciągła (napisalem funkcje klamerkowa) tak miałem na zajęciach i to mi się kompletnie nie zgadza, bo w tym drugim przypadku f. 1/x również ma dziedzine bez zera......

Cami: help help help help help help

PW: Nie, teraz jest sensowne pytanie o ciągłość w zerze. Sztucznie nadano wartość f(0) = 1, zatem f jest określona dla wszystkich x∊R. Jest nieciągła w zerze, gdyż − mówiąc "słowami" − dla x > 0 wartości mogą być dowolnie duże, a dla x < 0 wartości mogą być "dowolnie duże ujemne", a więc w najbliższym otoczeniu x₀ = 0 można pokazać takie x, dla których f(x) różni się dowolnie od f(1) = 1.

Cami: nie rozumiem: "...a więc w najbliższym otoczeniu x₀=0 (czyli pkt (0,0)?) mozna pokazac takie x, dla ktorych zbior wartosci rozni sie dowolnie od f(1)=1 (skąd to?)"

Cami: PW

PW:

	1		1		1
Trzeba np. skonstruować ciąg x1 = 1, x2 =		, x3 =		, ... xn=		, ...
	2		3		n

f(x_n) = n − im bliżej zera podchodzimy w dziedzinie liczbami x_n, tym bardziej f(x_n) = n różni się od f(0)=1 − wbrew definicji ciągłości funkcji w punkcie.

Cami: nie......... nie wiem o czym mówisz.........

PW: Policz samodzielnie i porysuj − zobacz jak x_n zbliżają się do 0, i jak f(x_n) oddalają się od 1 (a powinny się też zbliżać). Więcej nie mogę Ci pomóc.

Cami: znaczy się to że ciąg zbliża się do 0 to to widzę, ale z tą funkcją to już nie za bardzo... staram się na wszystkie strony, ale tego f(0)=1 nie widzę:(