wykres sin|x| ***: czy wykres funkcji sin|x| jest okresowy? mi wychodzi, że tak. proszę o weryfikację

daras: no pewnie

***: dzięki wielkie

Gray: Jesteście pewni? sin|x| jest nieróżniczkowalny w zerze − to jedyny punkt w którym jest nieróżniczkowalny. A gdyby był okresowy to..... − dokończcie sami

***: no tak, tylko my na studiach jeszcze różniczek nie przerabialiśmy. jeśli dałoby się to jakoś obalić nie na podstawie różniczek to tak, ale mi okres wyszedł π

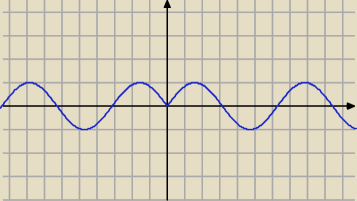
Gray: Teraz nie mam czasu na nic więcej za wyjątkiem wykresu. Musze lecieć na zajęcia. Może wieczorem, jak problem będzie aktualny..

J : .. to zobacz,co się dzieje z wykresem w pobliżu osi OY ...

J : o właśnie .. to co narysował Gray ..

***: to wieczorem gdybyś mógł to lepiej wytłumaczyć to byłabym wdzięczna

***: no dobrze, tylko jak to rozpisać. czy narysować wykres tylko skoro nie mieliśmy różniczek

Gray:

	π		π
sin		=1, sin(π+		) = −1 więc π nie jest okresem
	2		2

PW: Nic takiego nie trzeba wiedzieć. Punkt x₀ = 0 ma taką własność, że w jego niewielkim

	π		π
otoczeniu, np. dla x∊(−		.		) funkcja f(x) = sin|x| przyjmuje wyłącznie wartości
	4		4

dodatnie, zaś f(x₀) = sin|0| = 0. Widać to na rysunku Graya, który powinien umieć wykonać każdy licealista: − dla x > 0 f(x) = sinx, a dla x <0 f(x) = sin(−x) = − sinx. Z własności funkcji sinus wynika, że nie ma drugiego takiego punktu x₁ (ani po prawej, ani po lewej stronie x₀), dla którego byłoby sinx₁ = 0 i jednocześnie dla wszystkich dostatecznie małych α wartość sin(x₁−α) miałaby taki sam znak jak sin(x₁+α), gdyż jak wiadomo jedynymi miejscami zerowymi funkcji sinx lub sin(−x) są liczby postaci kπ, w otoczeniu których funkcja ta zmienia znak. Skoro nie ma drugiego takiego punktu w otoczeniu którego funkcja f ma takie same wlasności, to znaczy że f nie jest okresowa.

Gray: Albo tak: ponieważ dla x>0 sin|x|=sinx oraz dla x<0 sin|x|=−sinx zatem jedynym sensownym kandydatem na okres jest 2π. Ponieważ jednak

	π		π		√2
sin|−		| = sin(		)=
	4		4		2

oraz

	π		π		√2
sin|−		+2π| = sin(−		+2π) = −		,
	4		4		2

zatem nic z tego.

MQ: Po prostu ~∃T∊R ∀x∊D_f (sin|x+T|=sin|x|)