Wysokość ostrosłupa prawidłowego trójkątnego tworzy z wysokością ściany bocznej Ardox: Wysokość ostrosłupa prawidłowego trójkątnego tworzy z wysokością ściany bocznej kąt alfa. Wyznacz objętość tego ostrosłupa,jeśli krawędź jego podstawy ma długość a. Pomóżcie proszę, podchodzę do tego już 5−ty raz i nie mogę sobie poradzić..

Raf131:

	a2 √3
Pp =
	4

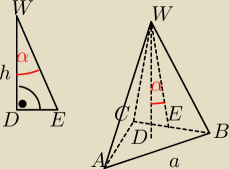
Punkt D jest punktem przecięcia się wysokości w trójkącie równobocznym, czyli

	1		a √3		a √3
|DE| =		*		=
	3		2		6

W ΔDEW mamy:

	|DE|
tg α =
	h

	|DE|		a √3
h =		= |DE| ctg α =		ctg α
	tg α		6

Szukana objętość:

	1		1		a √3		a2 √3		a3 ctg α
V =		h * Pp =		*		ctg α *		=
	3		3		6		4		24

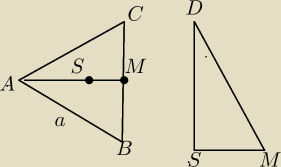
Ditka: SM=¹₃a ∡SDM=α tgα=¹₃a/H H=¹₃a/tgα V=¹₃*P_p*H P_p=(a²*√3)/4 V=¹₃₆*a³√3/tgα

Ditka: rzeczywiście SM=¹₃wysokosci trojkata wiec a√3/6 przepraszam ide spac

Ardox: Dzięki!